本文将向您展示哈希冲突的原理

combunion是一个去中心化的（DAO）组织协作网络，它为数字时代提供了新的业务基础设施和价值转换机制。它致力于使劳动价值像资本一样自由流动、交易和积累。

本系列包括：基本概念与原理、密码学、共识算法、钱包与节点原理、挖矿原理与实现。

本文致力于解释哈希冲突的原理，这对理解哈希算法非常重要。如果你彻底理解了这一点，那么散列算法的许多特性，包括为什么在区块链中使用哈希算法，都会被完全理解。

定义

抽象函数（hash函数）实际上是一个安全定义。

抗原图像碰撞

原始图像是什么？函数有定义域、词和对应关系。所以这里类比一下，原始图像是指定语义域中的某个未知数。

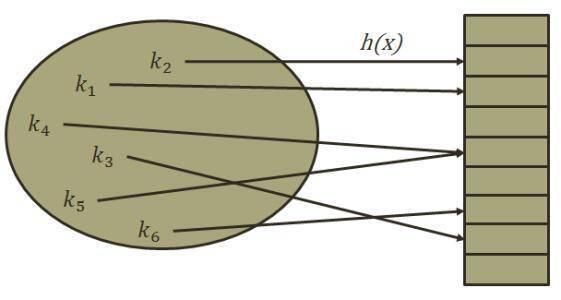
以hash算法应用中的挖矿实例为例，X为定义域，内部部分为原始图像，Y为值域。

让我们看看它的定义。几乎所有的消息摘要都很难用PPN算法计算图像。

如果确定了对应关系或散列函数，则在对定义域中的元素（例如x1）进行散列处理后生成散列值（例如Y1）。

假设此时产生了Y1，但没有告诉任何人。接下来有一个问题：Y1的原始形象是谁？

这是很难发现的，即提供一个图像：Y1，很难找到其对应的原始图像：x1，这是抗原图像碰撞的意思。

反二次图像碰撞

从字面上讲，有两个原语，很难找到它们之间的碰撞。

给定摘要函数H和消息M1，任何PPN算法都很难计算出M1≠M2和H（M1）=H（M2）的M2。

这意味着给定一个散列函数，通过任何PPN算法都很难找到M2，但是这个M2和M1中的图像是相同的，这是非常困难的。

防碰撞

给定一个摘要函数，任何PPN算法都很难找到M1，M2，因此h（M1）=h（M2）。

这意味着给定一个散列函数，使用任何PPN算法，都很难找到两条消息（原始图像），使它们的图像相同。

强防冲突是指给定一个哈希函数，从定义域（原始图像）中随机找到两个数字，两个数字具有相同的图像。这样的数字很难找到。

防二次图像碰撞与防碰撞的区别如下：

防二次图像碰撞是防碰撞中的一个特殊问题。由于两幅原始图像是随机选取的，并且期望的图像是相同的，所以抗碰撞条件更强。反二次图像碰撞就是给出一个固定的原始图像，然后再找到另一个原始图像，使两个原始图像相同。所以反二次图像碰撞是弱抗碰撞。

在区块链中，如果一个哈希函数满足上述三个安全定义，即：抗原碰撞、反二次图像碰撞和防碰撞，则可以使用该函数。例如，SHA-256符合这三点。

应用

通过对安全性的定义，其实我们可以发现一个特点：这个功能可以进行数据完整性认证。

你为什么这么说？

例如，**a发送一条消息：使用任何函数H，并使用SHA-256散列该段落。假设所有哈希值都为0，则生成256个零。

**a将此消息发送给**B。在接收到该消息后，**B还会“使用任何函数H”对其内容进行哈希处理。如果生成的值是256个零，则表示消息在传输过程中没有被篡改。

发送方将完整的传输传输给接收方，完成发送方的目的，接收方也可以验证数据的完整性。

有些朋友在这里有疑问，那么对于这个信息：如果你使用任何函数x，经过哈希处理，会生成256个零吗？

我可以负责任地告诉您，如果用于散列消息的函数满足上述三个安全定义，则不会发生这种情况。因此，在选择区块链开发的功能时，可能不使用SHA-256，但必须满足这三个安全条件。

其实说到这，很多朋友会有一个疑问：如果我用SHA-256算法，它原来的图像是任意字符串，像固定的，那么这个图像有多少空间？

答案是：256倍的2倍图像，也就是说，它可以容纳这么多的图像。

安全等级

还有一个问题：如果有任意数量的原始图像和固定空间较大的图像，那么可以肯定的是，通过一定的概率找到同一图像的两个图像，即会发生碰撞。这次碰撞的可能性有多大？

这个问题很容易理解。它似乎是固定的，但有许多原始的线路。在一个固定的空间里，必然会有碰撞的概率，比如前面提到的粒子对撞机原理。

很多朋友会被这个问题困扰很长时间。

事实上，密码学中有一个悖论来解释这个问题。让我们用“生日悖论”来解释这个问题。

生日悖论

上述成功概率与以下问题有关。

问题：你需要多少学生在教室里至少有两个同一生日超过0.5（50%）的学生？

直觉上，这至少需要2/365≈183人。但是，如果你仔细分析和复习你以前学过的概率论知识，你会发现这个问题并不容易回答。

从另一个角度来看，从反面解决这个问题可能会更好。

这个问题的负面事件可以理解为：教室里任意两个学生生日不同的概率大于50%。

如果我们能计算出负事件发生的概率，那么用1减去概率就是原来问题的答案。

所以这个问题就转化成：在这个教室里找到任意两个人生日，不同概率的人数大于50%。

那么有多少人不同，概率超过50%？

让我们做两个假设

假设1，每个学生在某一天生日的概率是1/365；

假设2，n个学生有不同生日的概率大于50%。

这就是n。

我们先分析一下n个人中两个人生日不同的概率？也就是说，如果从教室里随机抽取两个人，他们生日不同的概率有多大？

答案是：364/365。

换句话说，把两个人标记为a和B。如果a的生日是365天中的一天，那么B的生日与a的生日不同，有364种可能。

我们继续吧。三个人不同的可能性有多大？所以是：364/365*363/365。

……

那么n个个体不同的概率应该是：363/365*364/365**（365-n+1）/365

在这个时候，我们已经计算出n个人有不同生日的概率。如果概率大于50%，可以写为：Pro[363/365*364/365**（365-n+1）/365]gt；

5，这是消极事件的解决方案。

正面事件可以写为：1-{Pro[363/365]

*364/365*……*（365-n+1）/365]gt；0.5}gt；0.5

对N列式求解后，得到N≥23，即只要不少于23人，至少有两人同一生日的概率大于50%。

这似乎令人难以置信，但计算表明，在一个30人的班级里，两个人生日相同的概率是70%；对于一个60人的班级，概率大于99%。

从逻辑矛盾的角度看，生日悖论不是一种“悖论”但是这个数学事实是如此的违背直觉，以至于被称为悖论。

通过这个问题，让我们回到散列函数冲突问题：如果使用的散列函数是SHA-256，它的安全级别是多少？

换句话说，如果使用的散列函数是SHA-256，那么要使两个图像之间的碰撞概率大于50%，需要进行多少次计算？

通过生日悖论，我们可以理解SHA-256的安全级别不是2^256（2的256次方），而是：2^（256/2），即2的256/2次方。

实际上，在密码学中，hash函数有一个特殊的安全定义，它与hash函数的后缀有关。因此，如果使用sha-n，其安全级别为：2^（n/2）。