我们将先从数学家泊松讲起,然后推导泊松分布,**论证,为什么区块链的攻击者的潜在进展是一个泊松分布
。
1781-1840
),是法国
19
世纪力学家、物理学家与数学家。曾言
“
人生只有两样美好的事情,发现数学与教数学
”
,而他也确实做到了,既是一个**的科学家,也是一个**的教师。泊松的研究范围极广,几乎对所有数学分支都作出过贡献;对电磁理论的研究,实际上创建了数学物理的一个分支;物理学中理论力学、流体力学、热力学、弹性力学、外弹道学、天体力学等都有他的足迹。作为老师,曾培养了柯西等人,但也遗憾未能赏识阿贝尔、伽罗瓦。
——
立志数学
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
泊松解开这个有趣的数学游戏后,对数学如痴如醉,在自己的努力下最终取得了令人瞩目的成就。
——
泊松亮斑
17
世纪初笛卡尔提出光是波的看法,并得到了惠更斯的支持,波动说占了上风。十八世纪,牛顿发表《光学》,认为光是粒子,由于其崇高的历史地位,微粒说风行。十九世纪初,托马斯杨做了**的双缝干涉实验,证实了光是一种波。很多科学学家再次倒向了波动学说的阵营。但是粒子说还有很多坚定支持者,比如我们要讲的主人公泊松。
1817
年
3
月,提出了两个征文题目,作为
1819
年数理科学的悬赏项目:(
1
)设计实验证明光具有衍射效应;(
2
)依据实验用数学方法推导光通过物体附近的运动情况。
年,年仅
30
岁的菲涅尔(被后世成为
“
物理光学的***
”
)提交了应征论文,并给出了波动方程,完美的解释了光的偏振现象,定量的计算了光遇到圆孔或圆板时的衍射花纹,完美地符合实验观察。但是论文遭到了评审文员会(拉普拉斯、毕奥、阿拉果、吕萨克与泊松)中光粒子学说的支持者泊松的强烈反对。
泊松运用其高超的数学技巧,根据菲涅尔的理论,推导出了一个圆盘衍射的结论,若菲涅尔的理论是正确的,那么当点光源的光射向圆盘时,在圆盘后,距离圆盘特定距离的屏幕上,圆盘的阴影的中心会出现一个亮斑,这是多么的荒缪。泊松欣喜若狂,宣称自己驳倒了光的波动学说。
阿拉果、菲涅尔得到这一消息后,分别利用泊松的理论结果做实验,果然在圆盘阴影的中心发现了亮斑。这个亮斑,被命名为泊松亮斑,不知泊松作何感想。这一实验,有力的支持了波动学说。
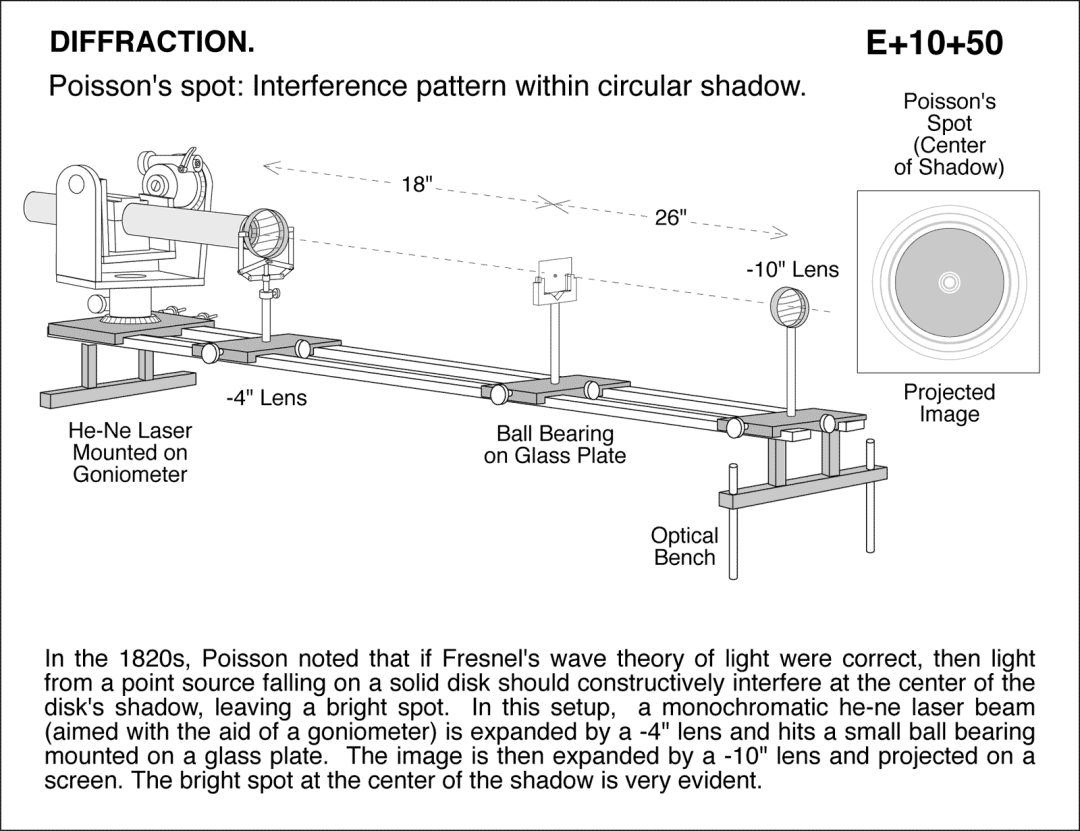
20
世纪,量子力学的蓬勃发张,揭示了光的波粒二象性,粒子说与波动说之争才告一段落。
——
泊松分布
DNA
序列的变异数、放射性原子核的衰变数,宇宙中单位体积内星球的个数,耕地上单位面积内杂草的数目等。还可用于指导商家如何备货,**化物流调运等,具有极其广泛的运用。
看似随机的现象,存在必然的规律。
泊松分布
。
均值,亦简称期望)是试验中
每次可能结果的概率乘以其结果的总和
,是最基本的数学特征之一。它反映随机变量平均取值的大小。
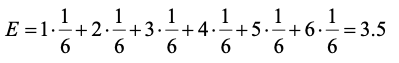
二项分布
伯努利试验中,设每次试验中事件
A发生的概率为p。用X表示n重伯努利试验中事件A发生的次数,则X的可能取值为0,1,…,n,且对每一个k(0≤k≤n),事件{X=k}即为“n次试验中事件A恰好发生k次”,随机变量X的离散概率分布即为二项分布(Binomial Distribution)。[百度百科]
(1)
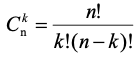
代表从
n
个不同的元素中,任取
m
(
m≤n
)个元素,可能的组合种类)。
e
,与几个极限
无限不循环小数,其值约等于
2.718281828459…,它是一个
超越数。它是怎么来的,怎么自然了?
——
自然对数
这个符号是以数学英雄
Euler
名字的首字母命名的,但是第一个发现这个常数的并不是欧拉,而是雅克比伯努利,而这个数的发现源自于人类的贪婪。
Alice
有
1
块钱,银行年利率
*
。如果
Alice
将这
1
块钱存入银行,那么,一年后她将得到两块。机智的你可能已经发现,年利率
*
,那么半年利率就是
50%
,如果
Alice
把
1
块钱存半年连同利息取出来,得到
1.5
元,然后再存半年,取出来会得到
2.25=1.5*1.5
。利息又产生了利息,
Alice
会比存一整年取出来多得
0.25
元。若变成一个月存取一次,一年后得到
2.613
。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
貌似存取周期越短,最终收益越高。如果存取周期为1/n年,1/n年对应利率为(1/n)**,n趋近于无穷时,Alice一年后总财富T会无限多吗?如果是无穷多,我们就可以采用这种策略,不劳而获了,遗憾的是,答案是否定的。
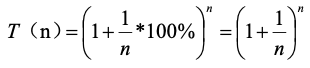
n
趋近于无穷时,
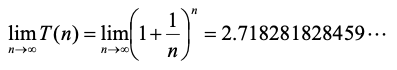
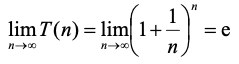
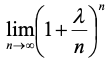
,令
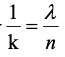
,即
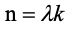
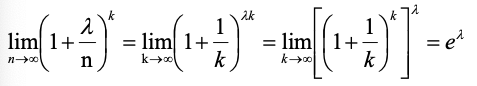
2
)
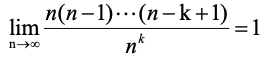
(
3
)
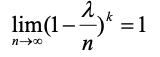
(
4
)
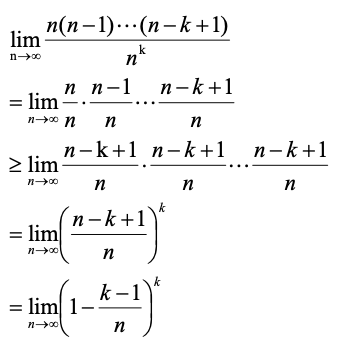
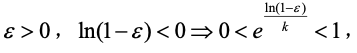
时:
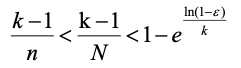
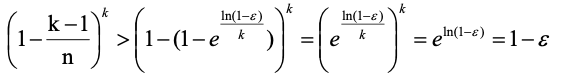
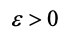
,都有:
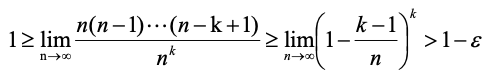
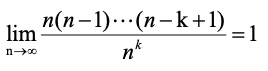
,(
4
)根据上述推导过程易得。
3.无后效性:在不相重叠的时间段内,事件的发生是相互独立的.
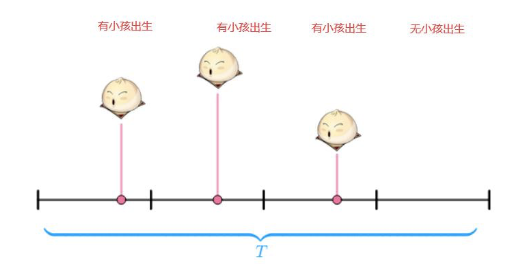
通俗来讲,如果对于事件A(例如一天内小孩的出生数量),我们把时间[0,1]平均分成n段,满足如下性质:
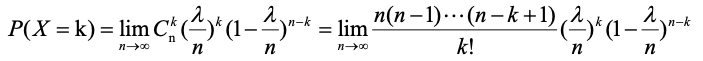
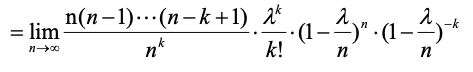 (5)
(5)
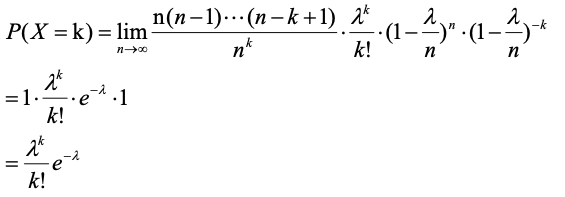
比特币攻击者与泊松分布
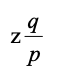
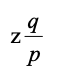
容易理解,但为什么是符合泊松分布呢?
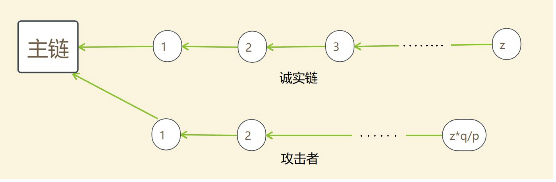
当诚实节点制造出
z
个区块,所需的时间期望为
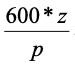
秒。(全网算力每
600
秒挖出一个区块,全网算力挖出
z
个区块需要
600*z
秒。诚实节点每次制造出下一各区块的概率为
p
)
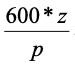
秒的时间,每秒看成一个时间段,分成
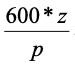
段。对于攻击者而言:

时间足够短,每个时间段
[i,i+1)
内只存在两种结果:攻击者制造出一个区块,或
0
个(
符合伯努利分布
);
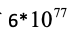
个数(这个数略微大了一些),只有
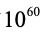
个正确答案,攻击者每秒能试
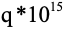
个。
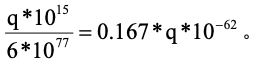
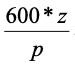
秒试过的数占总数的
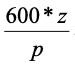
秒,无论攻击者何时成功制造一个区块,每一秒内成功的概率
P
都有:
z
个区块时,攻击者潜在进展就是一个泊松分布,分布的期望值为:
λ=Z*q/p
。
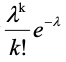
;攻击者取得进展区块数量为
k
时,落后诚实区块个数为
z-k
,能够追上诚实节点区块长度的概率为
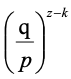
。
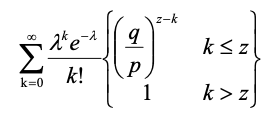
即:
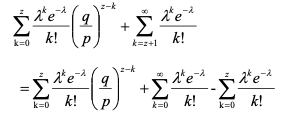
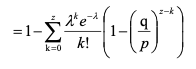
与白皮书上结论一致。
文章标题:比特币白皮书中的泊松分布
文章链接:https://www.btchangqing.cn/77003.html
更新时间:2022年10月13日
本站大部分内容均收集于网络,若内容若侵犯到您的权益,请联系我们,我们将第一时间处理。

