深度研究 逆向解构Curve V2

以为Uni V3 已经开启了AMM 通用兑换的巅峰，没想到Curve V2 是更为艰难的“冈仁波齐峰”。在为技术蝶变而惊喜的同时，我们更惊讶地发现这些头部DEX/AMM 项目正在走向一种“大同归一”的演变模式，就像今天要讲的Curve V2 实际上正是一种直接竞争Uniswap 的通用兑换模式，而在这之前不久，UniV3 也正式携全新的数学模向Curve V1 长期霸占的稳定币交易领域干涉和蚕食。本文尝试用逆向解构的方式呈现Curve V2 的基本数学原理。

基础模

简单来讲，CurveV2 采用了一种跟UniswapV3 非常类似的基本哲学——围绕“均衡点”聚集流动性。两者都并未依赖外部预言机来达成“均衡点”，而是依靠传统AMM系统内的交易博弈，直至系统均衡，在Uni V3里叫“职业做市商LP紧跟市场变化调整range”，在Curve V3中其命名为“内部预言机internal预言机”。作为两大最顶尖的AMM项目，可见其对任何外部风险都十分敬畏。虽然没有依赖外部因子，但这两种模，尤其是CurveV2，在通用兑换的道路上给出了非常优越的无常损失、中心化流动性、提升资本效率、低滑点、动态费用等一系列难题的解决方案。这当然得益于其“变态”的数学模。

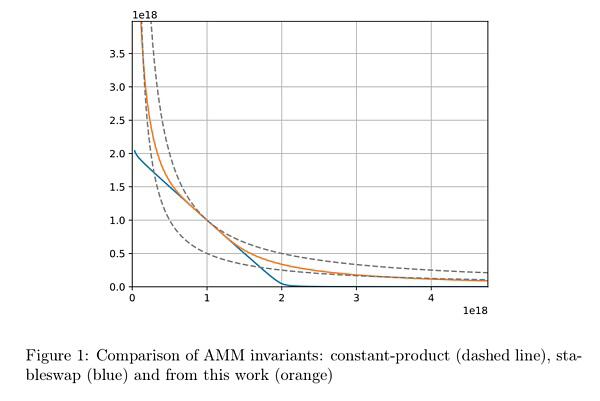
（图1）

数学模最核心的部分是其创造了一条全新形态的曲线。从上图直观来看，两条虚线是恒定乘积曲线，蓝色线是著名的Curve V1稳定币兑换曲线，而Curve V2构造的黄色曲线具备两个基本特征——

（1）介于恒定乘积曲线和Curve V1曲线之间；

（2）其曲线尾部特征拥有明显的恒定乘积曲线拟合。

所以它可以解决什么问题：

（a）继承了Curve V1在“均衡点”附近区域超低滑点和聚集流动性的优势；

（b）通过介于恒定乘积曲线和Curve V1曲线之间，以及在曲线的中尾部区域向恒定乘积曲线拟合，获得恒定乘积曲线快速响应流动性变化的优势，避免池子流动性枯竭，灵活响应快速的市场变化。

直接来看表达式：

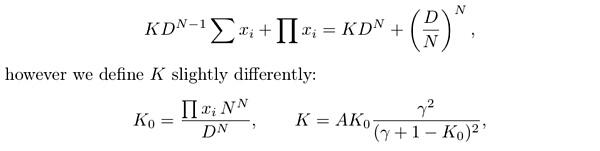
（图2）

乍一看十分晦涩，这里再引用一张KurtBarry 分享在twitter上的图：

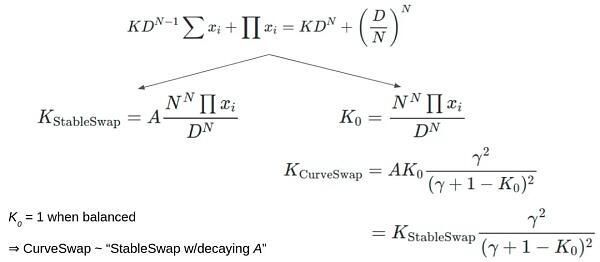
（图3）

稍微有点恍然大悟。没错，CurveV2 的“变态”曲线其实也是脱胎于Curve V1表达式。

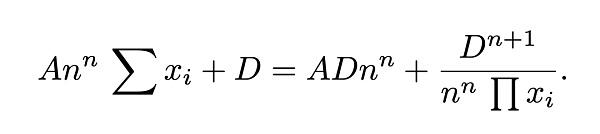
（图4：CurveV1 表达式）

当K0 趋近于1时，即从曲线形态上逼近“均衡点”范围时（对照图1 来理解），整个Curve V2表达式将退化为Curve V1表达式，使得兑换曲线拥有Curve V1的优良特性。

公式里最复杂的引入变量是gamma，它的由来要从图1中的两条恒定乘积曲线来讲。上方恒定乘积曲线与Curve V1表达式共同成就了V2曲线的“均衡点”区域范围，而下方恒定乘积曲线是对上方恒定乘积曲线的一个参数化缩小，即

上方恒定乘积曲线：

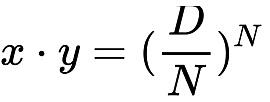
下方恒定乘积曲线：

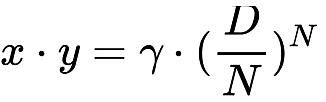
gamma是一个很小的正小数，在曲线形态上会比上方曲线更缩进原点。如前所述，CurveV2 需要引入这么一条gamma曲线，使得V2 曲线摆脱V1曲线在中、尾段的劣势（流动性枯竭和快速响应汇率变化），也就是让曲线拥有更大的后半段曲率。在这个基本原理的指引下，我们需要逆向来理解表达式的构成——

当坐标变化不断向横纵坐标轴的远方移动时，越趋近无穷大，V2曲线形态越向下方恒定乘积曲线拟合。即K0 趋近gamma，CurveV2 表达式reduction：

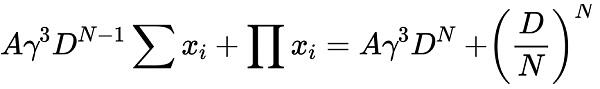
移项：

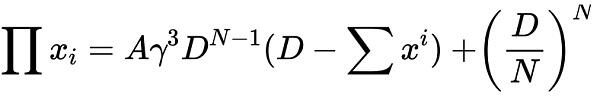
很明显，这将是一条偏向下方恒定乘积曲线的新曲线。

在这里，我们暂时只能从混合曲线的基本构造原理出发，逆向来解释Curve V2表达式的构成缘由，即以极限的思想分别向“均衡点”范围逼近以及向横纵远端逼近，表达式会分别reduction为Curve V1和恒定乘积曲线，以此来实现Curve V2将Uniswap 和Curve V1融合的目的，使得这种复杂混合曲线可以支撑通用兑换，并且具备更好的中心化流动性和滑点优势，同时保留Uniswap对流动性的保护以及对市场汇率突发变化的响应优势。

内部预言机

其实Curve V2还有一项非常重要的创新——内部预言机repegging机制。这项机制对实施更好的中心化流动性以及减缓无常损失是十分有利的。

Curve V2 引入了一种price_scale的价格度量，比如池子中有USDT 和B_token两种资产，balance为b=[1000,500]，汇率上1 B = 2USDT，则price 为p=[1,2]，最后相乘获得一种scaledbalance 为x=[1000,1000]。

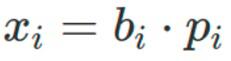
结合图1，在均衡点处，scaledbalance 序列内元素相等（恒定乘积特性）——

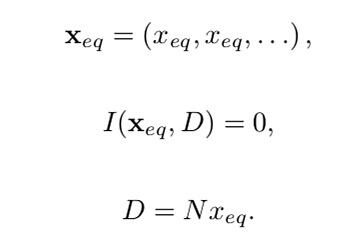
随着市场汇率的变化、兑换的发生、LP做市行为的影响，系统坐标点会逐渐偏离原始“均衡点”，如果不加以纠正曲线形态，不仅会造成流动性的聚集性减弱，还会带来无常损失。CurveV2 为此提出了MarketPrice Update 机制【1】——

i)exponentially moving average (EMA) price 预言机

ii)profit measurement

iii)repricing algorithm (depends on i and ii)

概括来讲，系统会通过经典的内部预言机机制EMA不断捕获系统内汇率的移动序列，然后不断在每一次交易和做市行为后根据price预言机 来更新一种名为收益度量（profit）的变量Xcp。

这种变量可以理解为每一次价格偏移距离原始均衡点的幅度，可以直观理解为，如果汇率变化幅度不大，系统公式将依旧以原始均衡点为根基，如果汇率变化非常大，坐标点在曲线上偏移很大，则系统应该重建公式，更换新的“均衡点”根基，以此来缩小无常损失和重新聚集流动性。Xcp这个变量便是用来量化合适可以更换公式和均衡点的手段。

如上所述，当Xcp突破阈值后，系统会根据此时更新的预言机price 来更新price_scale，以此来为新公式定位新的均衡点位置，随后更新新的D值，获取新的表达式。

这样，原本固定的Curve V1曲线便会随着场内汇率的大偏移不断变换均衡点，使得永远在当前汇率附近具备最大的流动性，及时对抗套利者，减缓无常损失。论文中有关于此项机制非常详细的参数化定义，也是实现的复杂之处。

总结

Michael Egorov一如既往地不愿意多说，所以我们看Curve V2非常晦涩。本文介绍了V2引领性的两大创新机制：新曲线和repegging。这条新曲线不仅静态复杂，还拥有了动态属性，可以根据EMA 和Xcp智能响应系统偏移，让池子流动性最大化地聚集在当前汇率范围内，极大地提高了动态资本效率，这是可以超越Uni V3的地方。我们最终会发现，CurveV2 可以与Uni V3再组合。