zkswap团队解读：zksync中的betterbetterHow to implementation aggregate proof

我们在zksync中读得比较好，我们知道如何实现单进程和聚合进程的电路逻辑。在本章中，我们将继续研究zksync的聚合证明，重点研究如何更好地形成聚合证明。

或者上一章中的代码图，我们将讨论create-again-proof

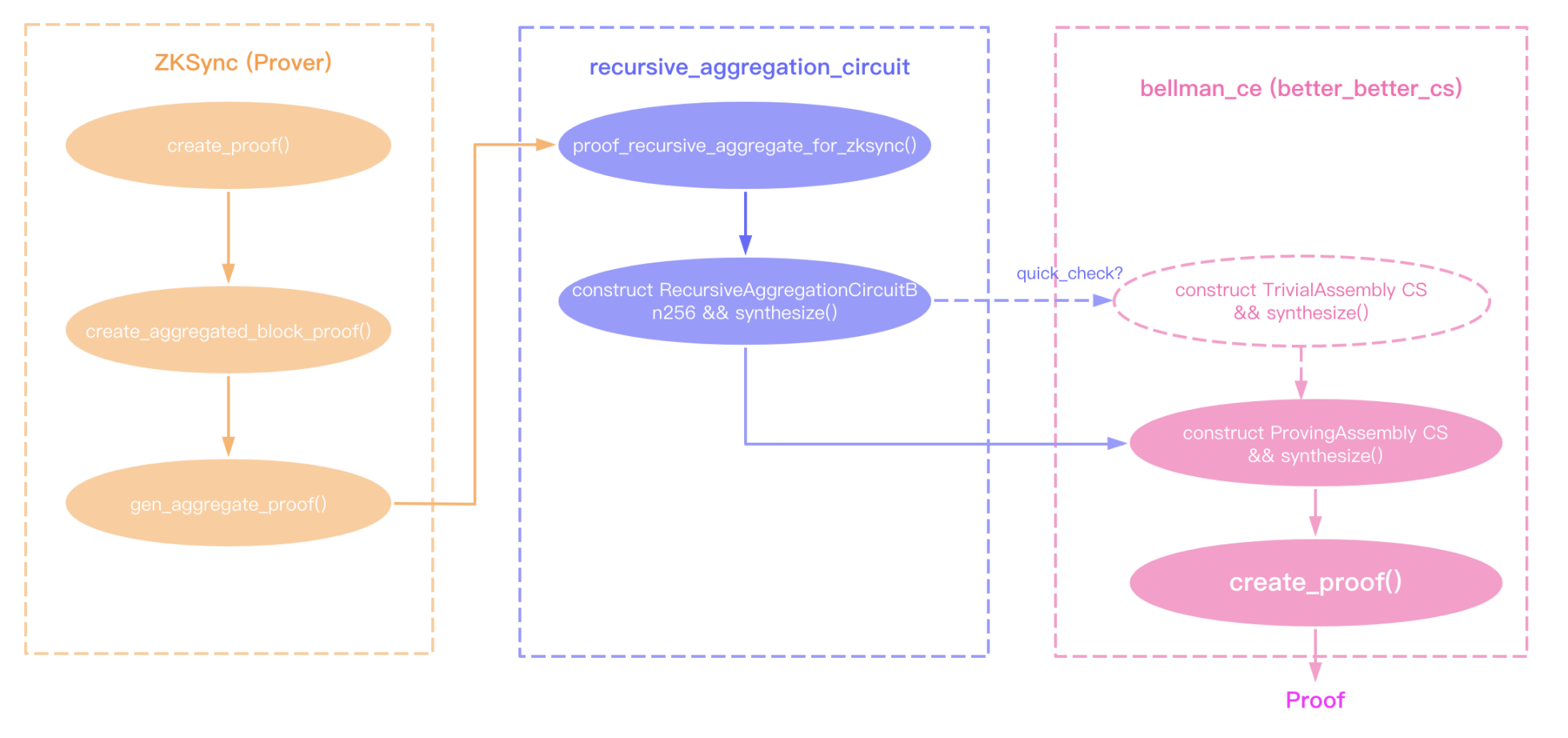
我们分析的行李员代码版本是beta，提交ID是48441155ec7006bf7bfac553b5fb7d466d7fcd00。证明的成功

createProof是bellmance/src/plonk/betterbetterCS/Proof/mod.rs中的一个函数，将近2000年⾏ 代码。

在车身上，分为以下步骤：

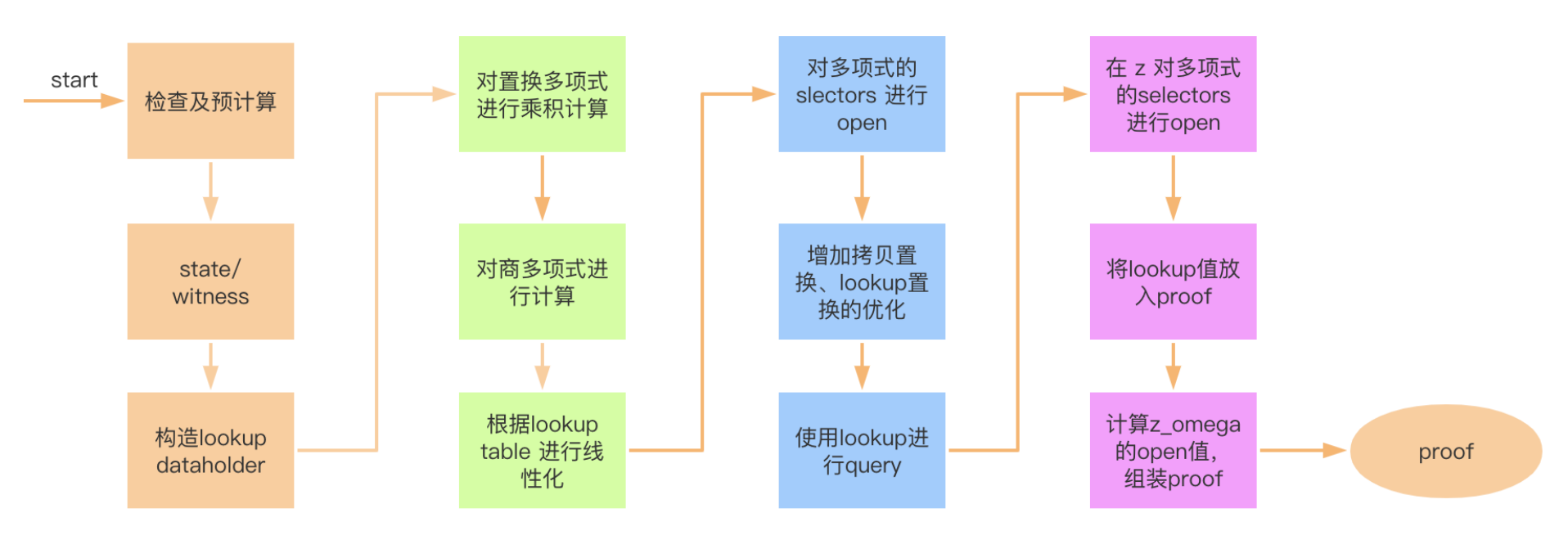
1.基本检查和预计算

2.为状态多项式状态和见证多项式状态，查表参数为排序多项式

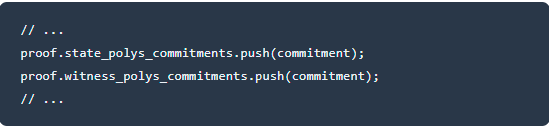
3.构造LookUpdateHolder进行后续计算

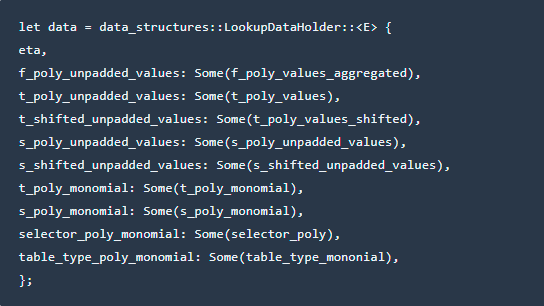
4.计算置换多项式的积

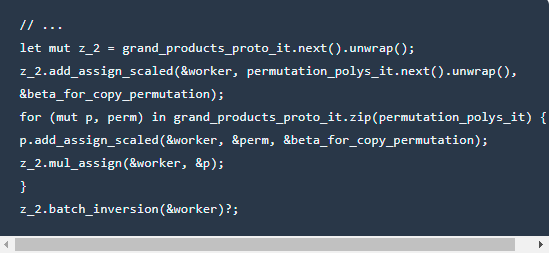
5.计算商多项式

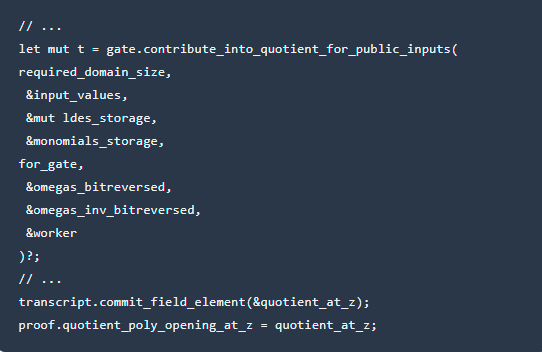
6.根据查找表进行线性化

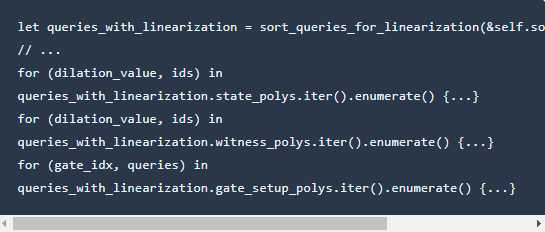
7.多项式的选择器取为⾏ 开放值

8.添加**置换多项式和查找置换的优化结果

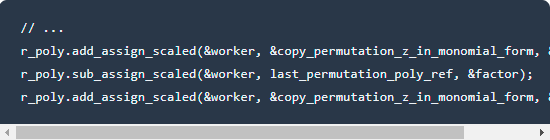
9.将“查找”改为“查询”

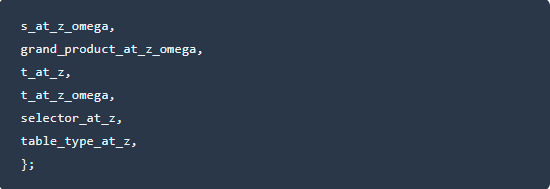
10.多项式的选择子在Z中取值⾏ 打开

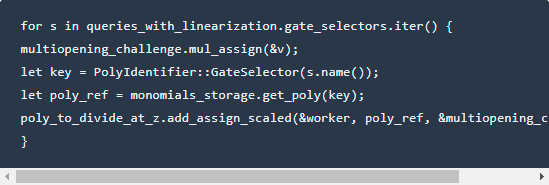
11.将最终查找值放入⼊ 证明

12.计算Z，ZΩ处的开度值，**组装证明

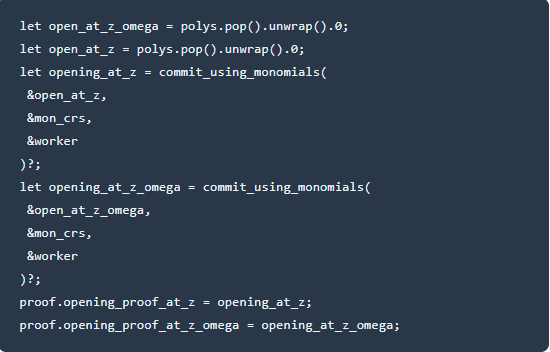
在这个函数中，我们看到了熟悉的Maingate函数。从上一版本如何实现聚合，我们知道基于的设计可以实现自定义门和优化电路。除了自定义gate之外，plonkup（plonk+lookup table）还用于zksync以提高效率。

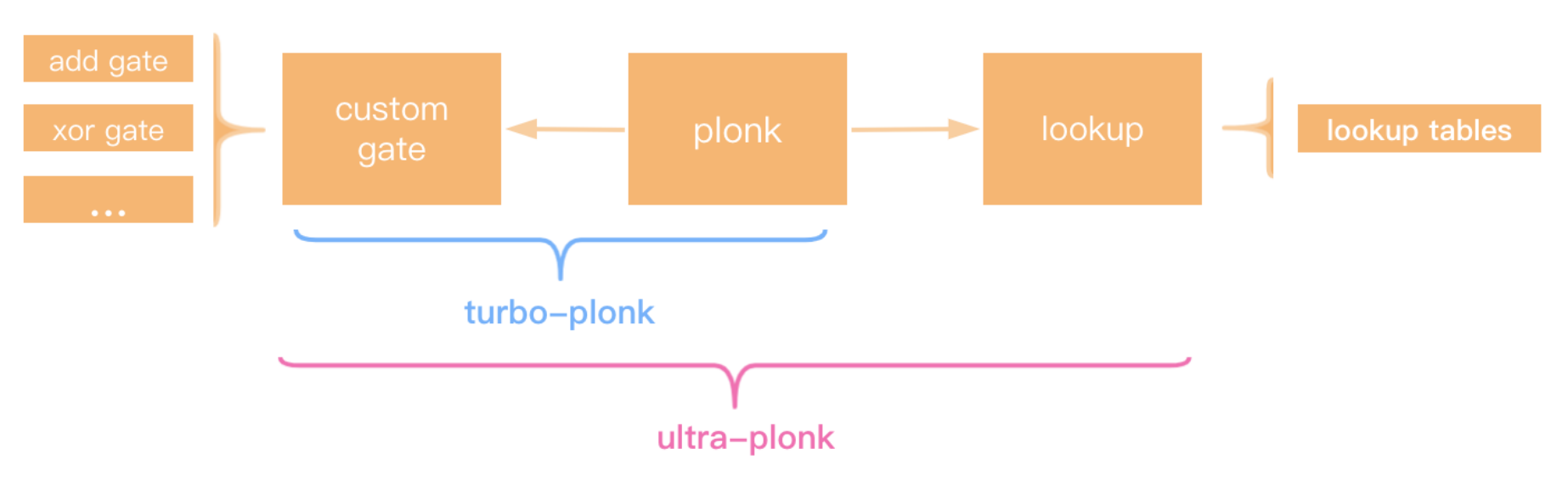
在上一章中，我们已经解释了plookup的原理。简单地说，高效的输入/输出被预先计算以形成查找表。证明人需要证明本表中的证人。有关详细信息，请参阅ZKSAP团队来解释plookup原则。Zksync对plonkup的实现并没有将自定义门和plonkup分开，而是将它们结合起来优化电路设计。让我们看看Maingate trait中的连接是如何与plonkup相结合的。

查找的使用

在上一节的证明函数中，创建线性化⽤ 到；参与公共输入的线性化；函数，让我们以它为例来看看查找的函数。此代码位于bellmanuce/src/plonk/betterubetterCS/CS.rs中。

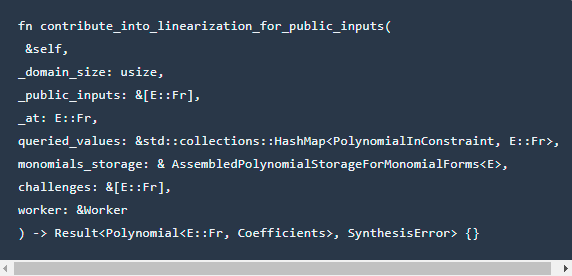
接收到的参数以HashMap格式进行查询｜值、单项式缓存值、请求的随机数数组｜值参数在｜中创建｜在证明过程中，根据排序后的查询列表生成。关键字是多项式，值是fr。查询列表的排序规则是见证优先，选通选择器第二，选通设置第3sortedgatequeries的结构如下：

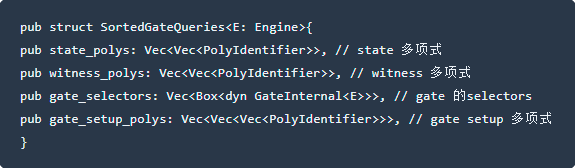
在代码中，调用⽤ 为线性化排序查询；职能部门；SortedGateQueriesnbsp此功能也在当前；卢比；⽂ 成片的。此函数的输入参数为；大门；数组，输出为；SortedGateQueriesnbsp

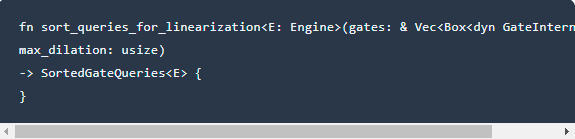
函数将传递给⼊ 大门；数组遍历，根据；大门；返回多项式数组，根据；变量多项式、见证多项式；**设置多项式；多项式存储在⼊ 分类分类查询；在中间。

返回；参与公共输入的线性化；函数，如您所见，它从查询的 In值开始，得到a/B/C/d的值。⽽ qa/qb/qc/qd/qu M的值来自create，lookup table的概念也来自证明的单项式缓存数据。

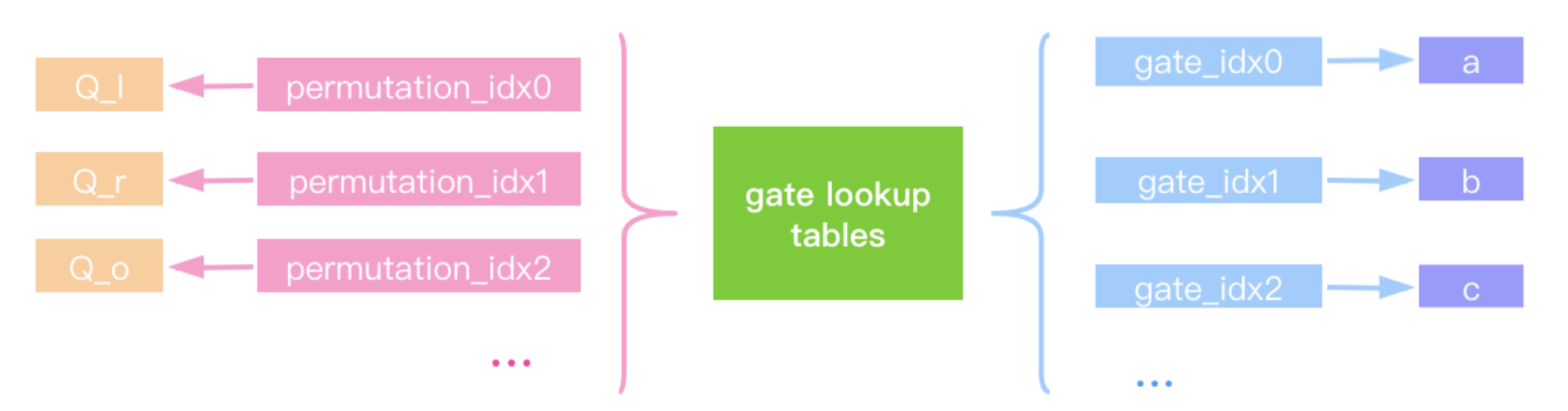
这个单项缓存的值是从电路的设置中获得的，也就是说，如果确定了电路，那么⻔ 确定了电路的工作原理。当⽣ 这些数据已经存在。您可以直接将安装预计算的结果放入⼊ 查找表并查询⽤ 数据。

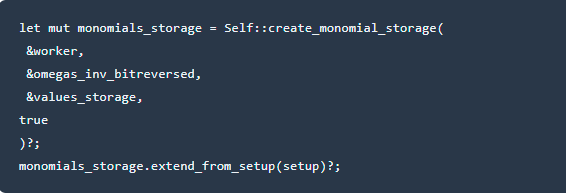
**，将a/B/C/D与Q挈a/Q挈B/Q挈C/Q挈D相结合。我们可以很容易地构造多项式。

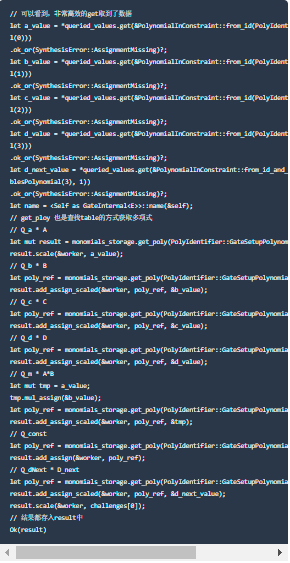
此外，⼏ 主门的连接功能⾥ 都是吗⼝ 就像。结合查找表，⾮ 可以很容易地计算出多项式。

总之，zksync将witness和gate的选择器和设置放入“查找表”。在生成“证明”时，“查表”可以直接查询“证明”，而不必重新计算，从而加快了“建立”速度，提高了验证程序的效率。

介绍

https://github.com/matter-labs/zksync

https://github.com/matter-labs/bellman

https://eprint.iacr.org/2020/315.pdf