AMM的通论：除了常数积之外，其他数学函数能减少无常损失吗？

本文研究了自动做市商AMM的一般理论，以期找到改善波动损失的方法。

原题：万向区块链首席经济学家邹传伟《AMM
通论》

以Uniswap为代表的常数产品AMM在加密资产市场取得了巨大的成功，但同时也承受着不稳定的损失。一些项目试图在Uniswap的基础上进行改进，如引入预言机报价以减少无常损失，但目前还没有公认的成功的改进方案。

为了更好地理解这些问题，我们需要回到AMM的一般理论：1。除了常数积公式，我们还可以取其他的数学函数吗？这些数学函数应该满足什么要求？2在其他数学函数下，会不会有无常损失？3什么是**的数学函数？4AMM与加密资产市场其他交易模式的核心区别是什么？

本文试图回答这些问题，全文共分为三个部分：第一部分讨论了AMM的一般形式，第二部分讨论了AMM的一些特殊形式，第三部分将AMM与加密资产市场上的其他交易方式进行了比较。

AMM的一般形式

为了简化分析，本文只对两种加密资产的AMM进行了研究，但很容易将相关研究扩展到三种或三种以上加密资产的情况。

考虑两种加密资产，分别称为X和Y，以加密资产X为记账单位，即所有的价格和市值单位都是加密资产X，AMM的状态是流动性池中两种加密资产的个数，假设在某一时刻为（X，Y）。在AMM的一般形式中，无论两种加密资产如何交易（无论交易费用的影响，下同），流动性池始终满足要求

当流动性池状态为（x，y）时，流动性池中两个加密资产的市值之间的关系为（x，y）

（1） （7）从不同的角度对AMM进行了表征，它们是等价的。换句话说，AMM也可以通过限制流动性池中两种加密资产的市场价值之间的函数关系来定义。

（8） 虽然这是一个简单的分析，但它对于理解加密资产的市场价值有着丰富的含义。首先，即使加密资产数量不变，它们之间的交易也会改变它们之间的价格关系，从而改变加密资产的总市值。

概括地说，本部分分析了AMM的一般形式，并得出以下结论

AMM的几种特殊形式

根据第一部分的讨论，任何单调递减Convex函数都可以用来定义AMM。

为了便于与Uniswap进行比较，下面使用一个等价的表达式

（16） 结果表明，在相同条件下，α越大，抗渗损失越小。（15）的数值计算也证实了这一点（表1）

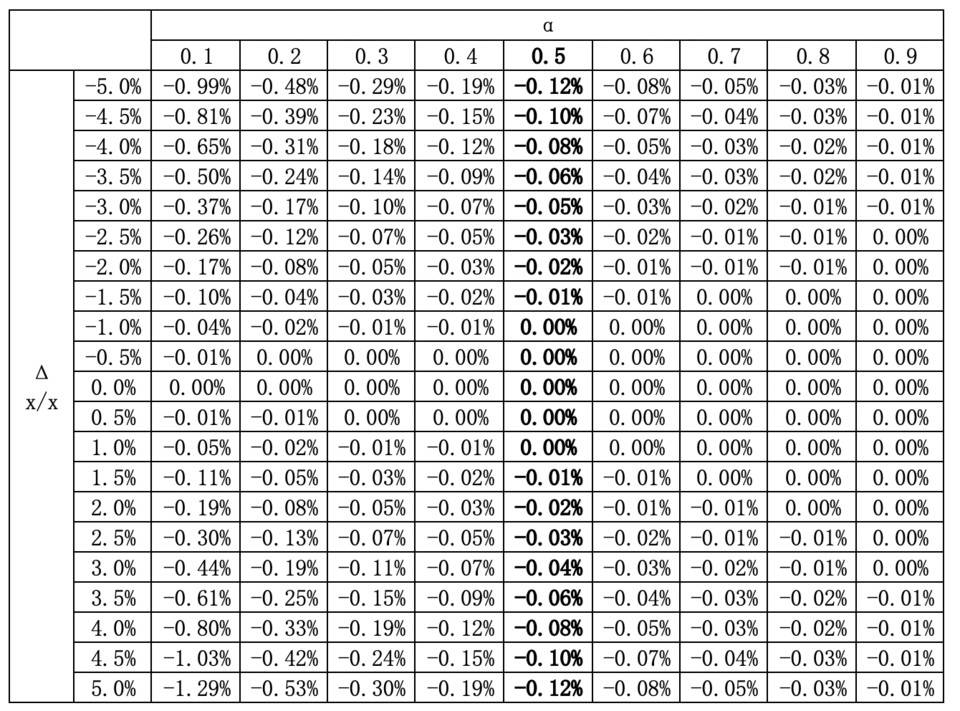表1：α对防渗损失的影响

如果α为1/2，则得到Uniswap的常数积公式，因此Uniswap属于广义AMM的特例。由于没有一对加密资产在基本面（如市场价值、流动性和用户数量）上完全相同，因此α=1/2在逻辑上并非不可避免。如果要减少无常损失，可以适当增加α。例如，如果加密资产x是稳定币，加密资产y是以太货币，则α可以大于1/2，并且一个选项是α=2/3。一般来说，α可以由AMM社区自治决定。

AMM与其他交易方式的比较

（2） 它可以等价地表示为

介绍了以下功能

一般来说，AMM的核心机制是流动性提供者基于算法承诺为投资者提供交易价格和交易数量的确定性。这种确定性的代价是流动性提供者锁定流动性并承担损失。

为了更好地理解这一点，我们需要将AMM与拍卖机制进行比较。在加密资产市场的各种交易机制中，只要存在指令簿，无论是否有做市商，其核心都是拍卖机制。接下来，以荷兰拍卖algorand为例。虽然这个例子是出售资产，但是前面的AMM分析是从购买资产的角度进行的，但是不同的角度并不影响分析逻辑。

荷兰式拍卖也被称为“出售拍卖”：卖家把价格从高到低叫停，直到有人愿意购买。在策略上，可以证明荷兰式拍卖等同于第一价格封闭式拍卖。在第一次价格封闭式拍卖中，所有竞买人同时提交密封投标，这样就没有竞买人知道其他竞买人的投标。出价**的人得到出价并支付他的出价。

荷兰在阿尔冈兰德的拍卖类似于美国国债的一级市场拍卖。荷兰拍卖在美国国债一级市场有着悠久的历史。1929年至1992年，美国财政部采用“多价格”荷兰式拍卖。第一步：主交易商提交他可以接受的到期收益率和他愿意在到期收益率上购买的数量。第二步：按照到期收益率由低到高（对应债券购买价格由高到低）对所有出价进行排序，直到愿意购买的数量等于债券的供应量，临界到期收益率为清算价格。第三步：到期收益率低于结算价的所有一级交易商将根据其愿意购买的数量获得债券，并根据各自的到期收益率计算购买价格。关键到期收益率的一级交易商根据他们愿意购买的数量分配剩余金额。因此，中标的一级交易商将以不同的价格购买债券。

自1992年以来，美国财政部已转向“单一价格”荷兰拍卖。“单一价格”荷兰拍卖的前两步与“多价格”荷兰拍卖的前两步相同。第三步，到期收益率低于清算价格的所有一级交易商将根据其愿意购买的数量获得债券，但购买价格根据清算价格计算。“单一价格”荷兰拍卖有两种拍卖方式：第一种是竞争性拍卖，即竞买人应同时说明其可接受的到期收益率和愿意购买的数量；第二种是非竞争性拍卖，即竞买人只需说明愿意购买的数量。对于两种类的投标，结算价格的确定方法同上。但在债券配额的分配上，引入了优先顺序：先满足非竞争性招标，再将剩余配额分配给竞争性招标，按提交的收益率由低到高分配至到期。

荷兰在阿尔冈兰德的拍卖相当于“单一价格”加上竞标。第一步是确定algo拍卖的数量和初始拍卖价格；第二步是随着时间的推移线性降低拍卖价格（图1），并记录每个拍卖价格上愿意购买的竞买人的数量，直到愿意购买的竞买人的累计数量等于拍卖数量，临界价格为结算价格（图2）2）第三步：如果拍卖价格高于结算价格，竞买人将获胜，algo配额将根据拍卖价格从高到低分配，该价格即为结算价格。

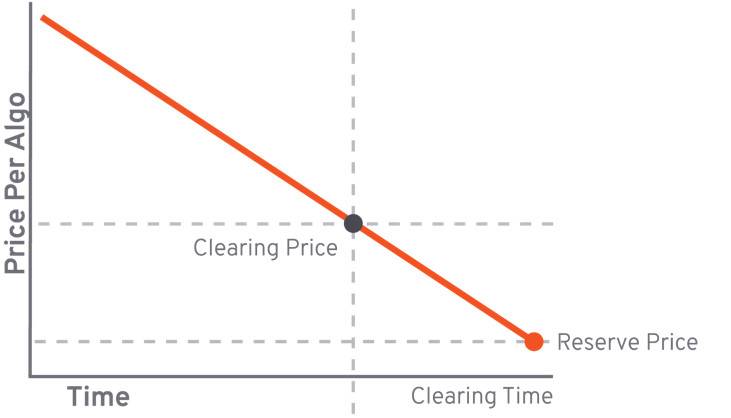图1:algo拍卖价格随时间线性下降

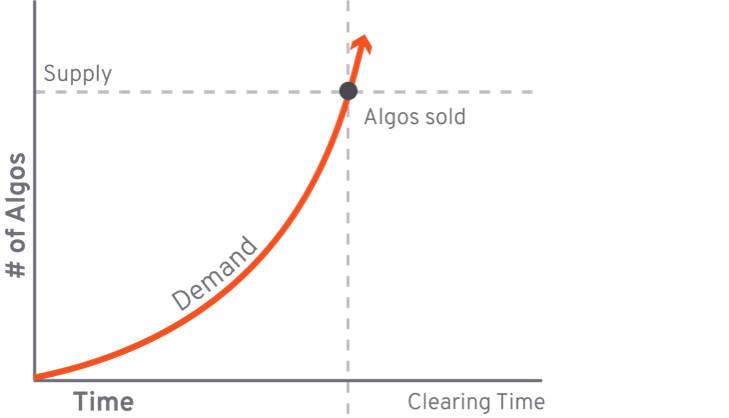图2:aglo结算价格的确定

从荷兰的拍卖实践不难看出，交易价格和数量是由市场决定的，市场事先具有高度的不确定性，AMM可以提供这种确定性。AMM与场内中心化撮合、场外询价交易等交易机制的区别，也可以按照类似的逻辑来理解。