解释uniswap v3中AMM的数学原理

前言：Uniswapv3（以下简称univ3）发布了许多特性，但其最本质的迭代仍然是对AMM数学曲线的重新思考。在过去的两年里，我们也参与了AMM领域。我们认为AMM最基本的曲线形状已经敲定，后续的创新应该是在AMM基本曲线形状的基础上进行“战略性”的，所以我们创建了mov超导v2。现在看到V3，我们突然有一种“再见你很久”的感觉。在寻找这种感觉的同时，我们也希望向您展示AMM最深刻的思想历程。因为AMM的时代将比想象的更加辉煌。

让我们直截了当地说，Uniswap V3最令人眼花缭乱的创新——中心化在AMM上的流动性。

V3给出了虚拟储备的概念

在传统的V2中，Alice一次性向储备池注入500000 Dai和333.33 ETH，总价值100万美元，提供全范围（0，/infty）流动性。但事实上，ETH的价格波动区间长期存在局部区间，极大地浪费了资金的利用效率。

（注：在逐渐成熟的金融市场中，无套利原则和提高资金利用效率始终是两大核心要求，也是后续DeFi产品挑战先锋DeFi的出发点。）

所谓中心化流动性，就是让LP选择波动区间，只为该区间提供局部流动性。例如，Bob认为未来ETH的价格区间为（10002250），如果未来ETH在这个区间波动，Bob希望获得和Alice一样多的收入，所以他只需要在一开始投资91751dai和61.17ETH，总价值为183500美元，远低于Alice的实际投资。让我们参考下图来解释原因。

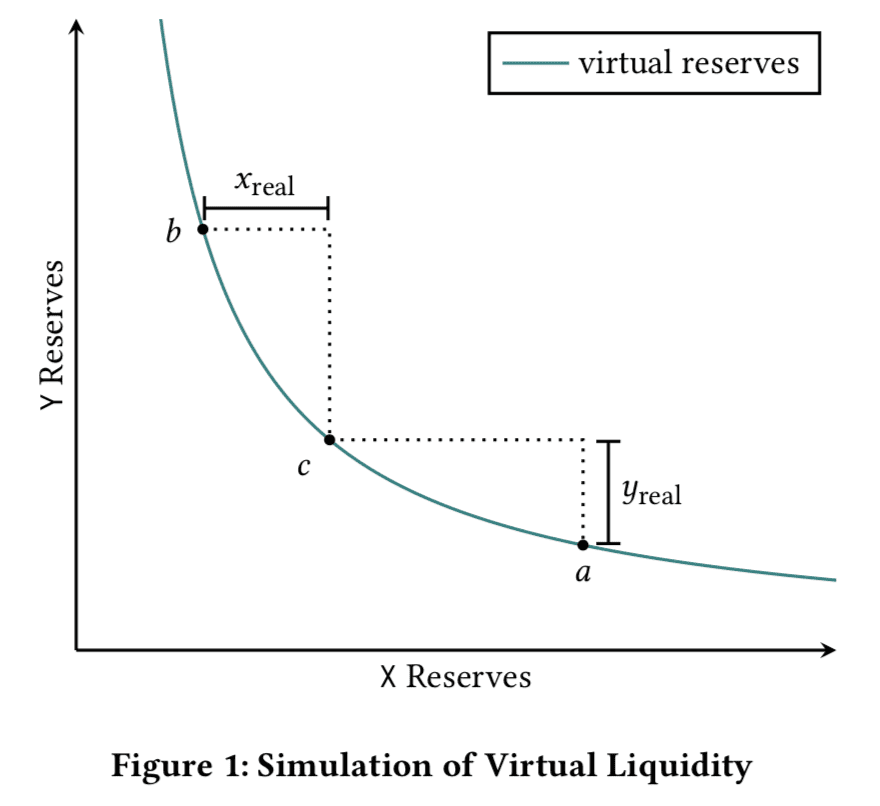
其中x是ETH，y是Dai，点a对应价格1000，点B对应价格2250，点C对应当前市场价格1500，x是Bob的61.17 ETH，y是91751 Dai。设d=6031为图中的虚曲线。
具有以下客观事实：

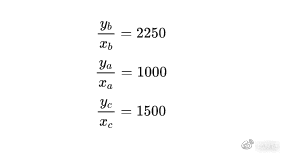
此外，由于

是

如何解方程

**，我们发现

也就是说，Bob得到的虚曲线（D值）与Alice几乎相同。
上述计算过程是一个反证。实际上，用户Bob会向系统算法提出自己的需求输入，包括预测价格区间的区间、当前价格点，以及最终的虚拟储量规模（即虚拟曲线D值）。通过虚拟曲线表达式的确定，我们可以很容易地计算出a、B和C的坐标，然后同时计算出X=17和y=91751.
，我们还可以看到，一旦未来价格超出范围，Bob的一项资产将完全消失。

虚拟准备金是Univ3中心化流动性的基本原则，也是Univ3将多种头寸统一成曲线的精巧部分。然而，这个看似简单的原理需要复杂的工程实现和算法模支持，特别是要解决费用的统计计算和LP加入/退出计算。
对于AMM，最复杂的是LP的访问行为和收入统计。在以V2为代表的经典AMM模中，LP各可提取量（包括手续费）的比例自始至终通过“份额模”确定。计算v3中“费用”的比例将非常容易。在
的实现中，univ3以滴答的方式将整个区域的价格转换为离散空间

如何根据当前的价格判断滴答声–

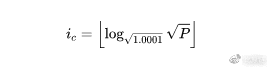
在全局状态下有feegrowthglobal0（f）和feegrowthglobal1（f）1，1）-f_1，用于从全局角度计算佣金收入总额。例如，当交易发生在一个勾号中时，系统会计计算交易的手续费：

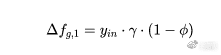
其中，y是交易的输入量，其余为手续费的比例。系统会持续累积每次勾选产生的所有手续费总和。
引入了一个“略低级别”的全局状态变量feegrowthoutside/-Fè，用于计算给定范围内的总处理费用。我们要查询一个价格区间（即下界勾I）和上界勾I，总公式如下：

其中，

f_u变量是高于I tick的所有区间的费用统计，f_u变量是低于I tick的所有区间的费用统计。因此，在上述通式中，我们从全球累计手续费总额F_u减去所有下限I，再减去所有上限I以上的费用，累计手续费为（I）u，I）两者之间的累计手续费。
f可以理解为一个计算单位，用于将服务费累计到I记号。在初始化过程中，我们同意如下：

让我们看一下，计算分为两部分–

如果当前勾号等于或高于I，则计算全局总手续费f uu从uu（I）中减去“累计到I勾号”的手续费f，其余为高于I勾号的所有区间的费用统计；

但是，如果当前勾号尚未到达I，则根据F琰，如果的初始化定义为0，则尚未生成高于I勾号的所有区间的费用统计信息，即0。

同样适用于F U–

如果当前勾号到达或超过I，F（I）代表累计到I的服务费，即所有低于I勾号的区间的费用统计；

如果当前勾号未达到I，则低于I勾号的所有区间的费用统计数据为当前全局变量F琰（当前总手续费）。

一般来说，系统算法需要统计一定范围内的累计手续费，

如果当前勾号已经在范围内，即q/leq ilt；i_uu，则只需从全球手续费F_u中减去所有低于i_u的费用，即公司形成的范围内的累计手续费；

如果当前勾号不在范围内，且低于下限I_u2，表示该范围内有交易，则不收取手续费，因此该范围内的累计金额为0；

如果当前刻度不在范围内并且高于上限I，则需要从全局总计中删除“两端”的相应累计量，即从全局F中减去所有低于I的区间累计量，减去“从I”到当前刻度区间。

univ3中服务费的计算过程是一种从微观到宏观的思考。它将空间划分为离散空间，每个时间尺度只在离散空间生成事务，从而产生服务费。每个微滴答记录自己从**滴答到本节累计手续费总额的变化，然后为上述公式不断调用计算各种宏观结果。
uni V3改变了AMM对LP行为的传统设置，不再根据全球流动性和份额计算每个LP的佣金收入。对于V3，只关注每个勾号中存在多少“虚拟”流动性，以及这些虚拟流动性产生多少手续费，从而计算出单位虚拟流动性对应的手续费。在这个时空中，我们可以将视角切割到每一个LP，对于任何一个LP，都会有一个“头寸”区间设置，它在自己的区间内提供虚拟的流动性。它可以是一个记号，也可以是多个连续记号。从最简单的“一勾”来看，系统会在同一时间和空间内记住每个LP注入的虚拟流动性值，并为它们确定一个比例（注意这个比例只与初始注入的虚拟流动性有关，不涉及将手续费转移到流动性，与V2）不同，以便分摊滴答中的所有累计手续费。

在实际应用中，LP将具有复杂的行为，如注入/退出的时间复杂性和选择的范围/滴答复杂性。然而，univ3最简单的部分是它使用全局计算来阻止单个LP透视图，并且只关心ticks透视图和position透视图。在确定了上述一系列全局状态变量的定义后，仔细记录每笔掉期交易的情况（包括只在一个记号中完成掉期交易，交叉多个记号完成掉期交易），只记录每笔记号中虚拟流动性的大小，从而从根本上提供掉期服务，即交易公式和掉期后服务费如何分配给所有参与交易的有限合伙人。线性规划问题的复杂性表现为空间的不连续性和时间的不均匀性。对于时间的不均匀性（即会有大量LP不断地加入和退出流动性），univ3还将引入职位级别的全局变量来记录每个身份（地址）的范围/刻度。未收取的feed/feegrowthinde确保后续的lp不会参与先前lp的累积收入分配。
综上所述，勾号级别是空间发生的统计，保证了同一起点的LP费用分配；位置级别是时间发生的统计，保证了不同起点的LP费用累计起点不同。为了真正获得安全的计算方法，建议实现者深入研究V3代码。
**，统一V3是太复杂，但主要道路是简单的。即使要模仿，模仿者仍然需要努力，才能深刻理解自己的“微积分”思想。本文仅从费用的角度提出univ3的“数学原理”，这也是中心化流动性的核心逻辑。除了数学，我们还有更多令人惊讶的“哲学”发现与大家分享，比如LP token的演变，NFT不仅在艺术领域（更有利于金融），V3将有一个战略游戏，V3对基金池/合成资产的启示等等。当然，它也包括AMM，mov超导v2的“心”，mov的本质是连续无限网。univ3在这种无限网格的基础上实现了微小的无限网格，即“众多网格机器人的叠加”。Mov超导V2在无限网格的基础上实现了宏无限网格，即超级网格。请期待下一个“univ3的自然哲学”。