理解cfmm（恒定功能做市商）的演变

在传统的金融市场中，每一种证券都需要一个买方市场和卖方市场来进行有效的交易。今天，股票交易的速度和简单性被认为是理所当然的，尤其是在新的Robinhood投资模式中。在这个新时代，做市商在为市场参与者创造无缝交易体验方面发挥着重要作用。在过去的一年里，做市商的角色已经以一种称为自动做市商（AMMS）的算法**的形式被移植到加密生态系统中。

AMMS与传统做市商的功能相同，促进了两种数字资产之间的交易。然而，在智能合约中，市场不是由大银行或贸易公司决定的，而是由算法决定的。与传统的依靠大量资源提供严格的买卖价差的做市商不同，AMMS重新定义了提供流动性的方式，并使用数学公式来确定资产交易的价格。

常函数做市商

恒功能做市商（cfmm）是***的AMM系列。当交易者想要将代币a交换为代币B时，该AMM将使用常数函数作为其定价机制。在这种情况下，术语quot;常量函数quot;意味着在任何交易中，资产储备的乘积必须保持不变。

自2017年以来，一些DEX修改了这个常量函数，以优化不同的用例。接下来，我们将介绍一些***的DEX，并详细介绍常量函数。

Uniswap公司

Uniswap是第一个流行使用常量函数（交换两个资产）的DEX。它使用了一个名为quot;的AMM变量常量积AMM quot;，它要求两个资产储备的乘积必须始终保持不变。

在这个等式中，X和Y表示流动性池中两种资产的单位数。例如，假设ETH/Dai池包含100 ETH（x的值）和10000 Dai（Y的值）。在本例中，Uniswap将这两个量相乘得到K值1000000。现在的目标是保持K的值不变，而不考虑流动性池的交易量。唯一的方法是反转X和y的数量。换句话说，当X的数量增加时（交易员将ETH添加到池中），y的数量必须减少（交易员将Dai从池中取出）。**，任何给定交易所的报价都是常量乘积公式和池中代币比例的函数。

应该注意的是，X和Y之间的关系不是线性的。1000 Dai的10 ETH不等于2000 Dai的20 ETH。相反，这种关系是渐进的。这意味着随着花费的代币数量的增加，接收到的代币数量减少。

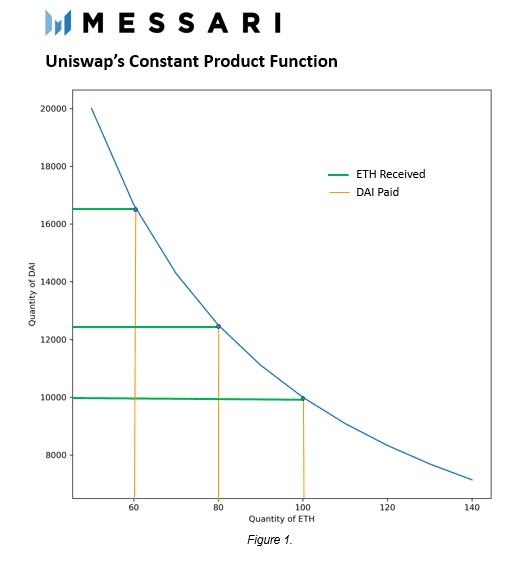
常积函数的性质对于资产管理系统是非常有用的，因为它保证了当任何资产的价格接近无穷大时，总是存在流动性。

平衡器

Balancer的AMM概括了Uniswap的常数积函数，并创建了一个名为a635常数平均值ammquot;的变量。该模的核心是价值函数，它规定资产池中资产余额的加权幂的乘积应始终保持不变。

在这个公式中，T表示池中资产类的数量，BT表示资产数量，WT表示资产权重。与Uniswap的简单的常数积函数相比，这个数学公式看似复杂得多，实际上却很容易理解。例如，假设用户创建了一个平衡器池，其中包含三种资产：100ETH、100btc和100000 Dai。每项资产的权重为33.3%。Balancer按如下方式处理这些值：

与Uniswap类似，其目标是在保持资产权重不变的情况下只改变资产余额，从而保持K不变。在余额池的情况下，交易可以在三种资产中的任意两种之间进行。用户可以使用ETH交换Dai，使用ETH交换BTC，或使用Dai交换ETH。通过保持K值不变，可以在这三种资产之间生成一个价值平面。

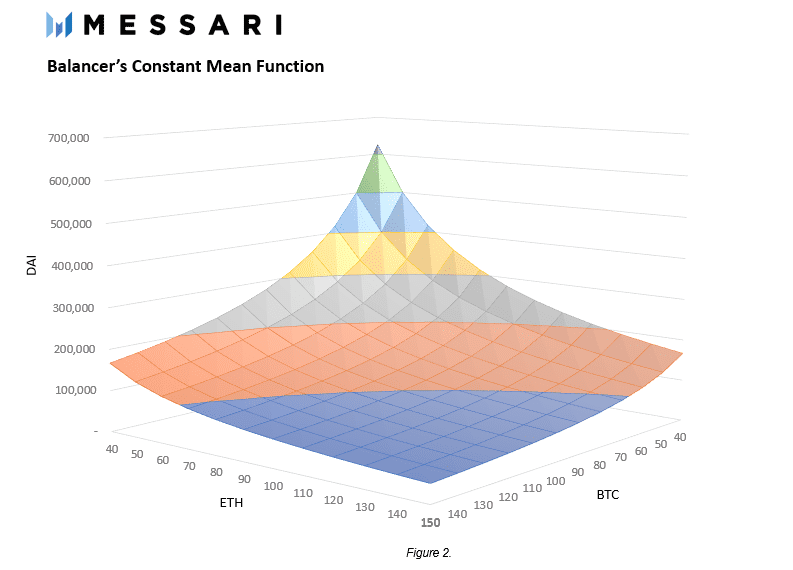
有趣的是，这个曲面与Uniswap的常数积函数没有太大区别。另一种思路是在图1中的常量乘积函数中添加一个表示池中第三个标记的额外轴。通过改变图2的角度，两个函数之间的相似性变得更加明显。

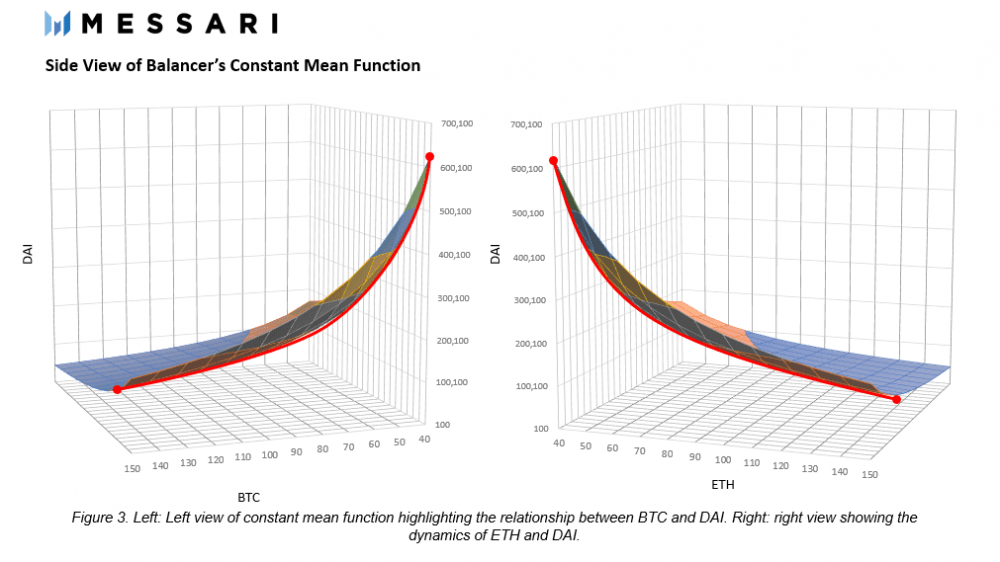
因为均衡器池被设计为有2到8种资产，所以任意两个代币之间的交易价格报价更为复杂。池中的每对代币都有一个价格，该价格取决于该特定代币的余额B和权重W。形式上，事务执行的价格是根据代币余额与代币权重的比率来计算的。

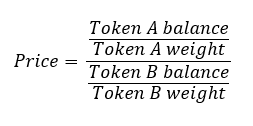
在上面的公式中，代币a代表卖出的代币（进入池），代币B代表买入的代币（离开池）。如果池持有人不改变资产储备，很容易看出价格变化完全基于交易，因为资产权重必须始终保持不变。这种机制与图2所示的常数面相结合，可以确保购买资产的价格将上升，而出售资产的价格将下降。与Uniswap一样，套利机会确保平衡器池提供的价格与市场的其他部分同步变化。

曲线

Curve是一个外汇流动性池，在这个池中，价格稳定的资产可以有效地进行交易（如稳定币或包裹的比特币）。Uniswap和balancer主要用于波动性和价格不稳定的代币交易。然而，在处理资产之间的交易时，希望彼此稳定，低价格滑动点是最重要的。在以前的迭代中，AMMS的固有曲率是有问题的，因为事务规模越大，滑动点就越大。

解决价格滑动点问题的一种方法是采用常和函数作为AMM的内部交易机制。当两种资产用于经营时，定和做市商强制规定资产数量之和必须保持不变，并遵循以下功能：

如图所示，双资横河做市商是一条简单的直线。

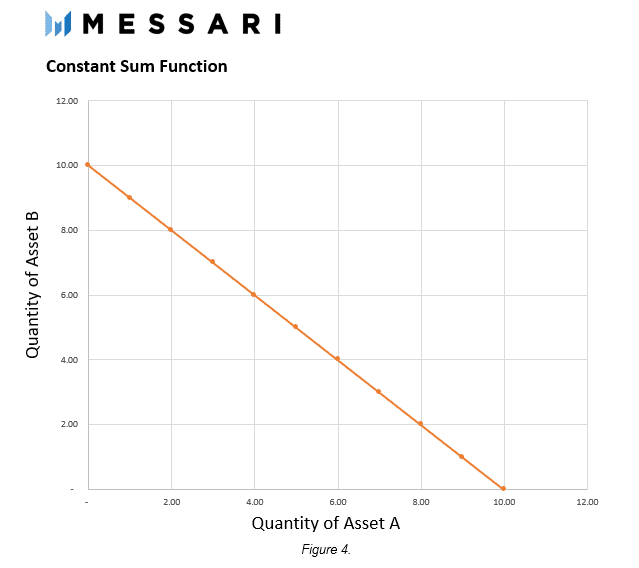
虽然这一函数的简单性达到了一个较低的滑动点，但它缺乏恒定产品做市商的关键属性，即当任何资产流出池时，池中总会有流动性，而另一种资产的数量往往是无限的。

为了解决这些问题，curve将常和函数与常积函数相结合，建立了一种混合AMM：在曲线的平衡点附近建立一条相对平坦的曲线，类似于常和函数，以保持价格相对稳定，并使两端更加倾斜，类似于常积函数，因此在曲线的每个点上都有流动性。在两个资产（x和y）的情况下，最终结果是以下复杂函数。

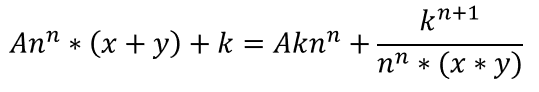
除了复杂的数学，注意两个常数函数是如何嵌入在方程中的。左边是常数之和，右边是常数的乘积。另外，为了达到预期的目的，在公式中还加入了其他一些项目。在公式中，n表示资产数量（在本例中，n=2），a是一个quot;放大系数quot;参数，它决定了函数和常积函数之间的相似性。a值越低，曲线函数越接近Uniswap函数。

与以前的cfmm一样，我们的目标是在交换x和y时保持K的值不变。绘制函数如下所示：

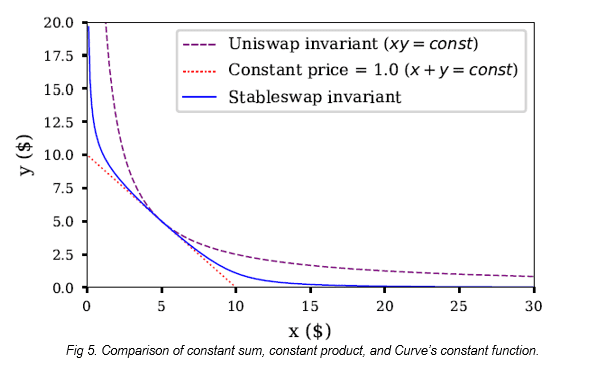
来源：曲线白皮书

从图5可以看出，曲线的函数中间是一个常数和函数，但随着X和Y值的增加，它变成一个常数积函数。这种形状在曲线中间保持价格稳定，同时在两端提供流动性。

结论

在过去的几年中，AMMS已经成为DeFi的一个重要组成部分，通过去中心化、全球可访问和非管理的方式汇集和提供流动性。具体来说，Uniswap、balancer、curve等cfmms实现了巨大的增长和应用，交易量超过数十亿美元。

自2017年以来，这些去中心化的交易所发展了各种不同的固定职能，以解决具体的交易所问题。随着这一领域的不断扩大，涵盖了各种资产，为了使交易更加高效，交易所必须对其基本功能进行大量思考。尽管这项技术仍处于早期阶段，但它带来了新的研究领域，更多的AMM设计将出现，最终为所有WiFi用户提供更好的移动性。