为什么一般的AMM模型不适用于期权定价？

要点：

1期权定价取决于多种因素（如到期日和隐含波动率）。在大多数情况下，它们通常为零（即非行权或无条件行权价格）。2一般AMMS（如Uniswap）的价格发现机制通常依赖于交易量。在流动性市场中，资产的价格应该由市场力量决定。然而，在本文发表时，DeFi期权市场还处于起步阶段，期权可能不会频繁更新，这将使期权价格过时，给期权池的流动性提供者带来巨大损失。3本文探讨了Uniswap V1背后的数学原理，并得出结论：Uniswap V1可能不是交易期权代币的最合适场所。

通用AMM和
通用AMM，如Uniswap V1和V2，是DeFi中最重要的组件之一。
模将价格发现和做市结合起来，使得即使是最缺乏流动性的资产也有市场和发展空间。
它精心设计了激励机制，鼓励不同的参与者作为卖方、买方和流动性提供者参与。事实上，流动性提供者是在系统中扮演重要角色的参与者。这感觉像是传统做市商的抽象概念。这种相似性背后的原因是AMM不需要连续的分类帐管理和订单填写，所以用户可以交易他们的资金。有些人可能会说，他们不是相同的用户，他们不是执行相同的业务。但归根结底，这两个参与者（Uniswap的流动性提供者和传统金融的做市商）都在引领一个市场。
目前，流动性提供者需要在资金池的两侧添加等量的资金作为流动性，作为回报，期望收取资金池中的所有交易成本，并收回其投资本金。
在DeFi中，一些用户总是将提供流动性的活动视为一种被动的收益性投资，即提供资产、持有资金、收取与初始资本成比例的费用。尽管这对于一个稳定的资产池（例如戴：USDC)这可能是真的，但在某些情况下（例如USDC：ETH)不完全是。在
中有一种现象叫做无常损失。间接损失（IL）是一个表达式，我们用来表示与仅持有两种资产相比，Uniswap在波动性资产对上增加流动性的负回报。
描述了寻求被动收入的流动性提供者的盈利能力受到负面影响的情况。如果添加的代币的价格最终能够恢复到添加到流动性池时的价格，那么无常损失就不存在或非常小。但是，如果价格情况与原始价格情况不同，与仅持有资产的情况相比，提取的金额可能少于后者的总额。
这意味着，只有当流动性提供者（LP）以不同于最初使用的价格状况移除流动性时，才会出现非**性损失。如果我们不撤走它，等待一个更机会主义的时机撤走，损失就不会发生。相比之下，在传统金融中，我们可以将其视为一种出售**性跨期债券的头寸。之所以它是可持续的，是因为这个职位没有到期日，LP可以持有它，只要它可以。

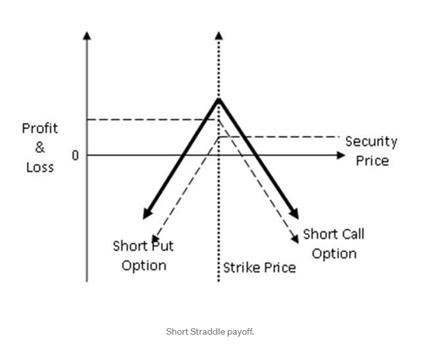
这意味着，即使在市场波动的情况下，如果LP在进入时消除价格水平的流动性，LP将受益于这一期间的费用，但不会遭受损失。
有些人可能会说，他们希望交易费用能弥补他们的损失。这是可能的，但仅在一定程度上，取决于撤资时的价格、资金池中有多少流动性以及在提供流动性期间发生了多少交易。因此我们可以理解，对于流动性提供者来说，最有利可图的投资组合是一个拥有非易变资产和每天大量交易的池。同时，我们也应该考虑到市场决定了资产定价。每当Uniswap中的代币定价偏离市场价格时，套利者就会利用这个套利机会进行Uniswap交易，帮助引导Uniswap的价格接近代币市场价格。

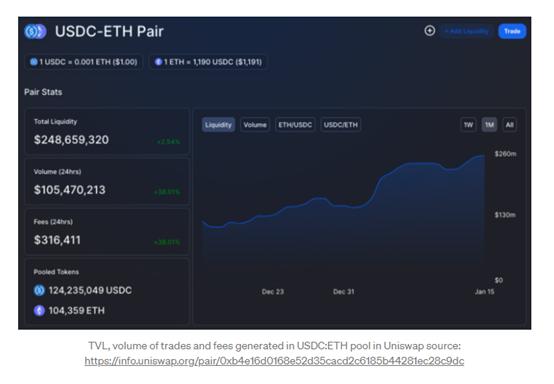
模拟收入
为了分析Uniswap V2上流动性提供活动的收入，应考虑以下变量：

在提供流动性时，交易对的现货价格、撤资时现货价格池中交易对的交易量以及池中资产量将分配给LP

常数乘积（k）因子是一种为交易定价并保持池两边价值平衡的方法。忽略成本时，系数计算如下：

定价
Uniswap使用以下定价公式定义流动性池中每项资产的交易价值。

将公式1和公式2放在一起，我们最终得到如下结果：

a6025
需要强调的是，在另一个LP向池中增加流动性之前，交易的资产定价采用常数。当发生这种情况时，常量将用新的池余额更新，并用于为后续事务定价。例如，
初始池有100个ETH和10000个Dai。因此，常数乘积（k）=100*10000=1000000。
如果一天后，John决定用2 ETH和2000 Dai增加池中的流动性（池中没有交易），则需要更新常数，因为流动性池的双方都增加了。因此，新的常数乘积（k）将用于对以下交易进行定价：k=（100+2）*（10000+2000）=102*12000=1224000。
考虑到Uniswap的AMM要求流动性提供者在每个交易对的充值中保持50/50的比率，公式2确定资产定价取决于每个池中的交易量。这意味着当池中没有交易时（池中发生的唯一活动是流动性准备金），价格将与池创建时保持相同。换句话说，只有在有交易活动时，价格才会更新。
当增加流动性时，资产的定价与你想从池中购买资产的定价不同。我们可以看到以下情况。例如，假设rob想向池中添加一对ETH:DAI流动性公司董事会成员。他想增加一个以太坊，但他需要提供多少代币？当前池余额为95 ETH和10529.49 Dai。根据公式5，他需要提供的代币数量=1*（10529/95）=110.87 Dai
。提供流动资金后，新基金池的余额为：

95+1 ETH=96 ETH10529 Dai+110.87 Dai=10640.36 Dai新k=96*10640.36=1021169.85

流动性提供者收入
为了了解Uniswap的AMM以及进入池时代货币的初始价格与退出流动性时代货币的价格之间的差异，另一个重要概念是LP token。
LP代币被转换成每个流动性提供者在池中拥有多少资金，然后每个LP将从池中产生的总费用中获得相应的收入。

无常损失
既然我们已经介绍了关键概念，让我们分析一下流动性提供者遇到无常损失的情景。
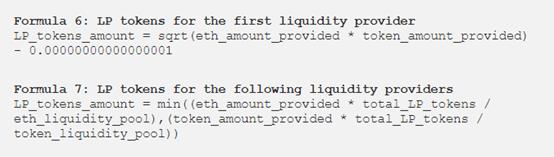
babi通过增加20K（100ETH和10000dai）的总流动性创造了一个新的流动性以太：戴池。作为第一个流动性提供者，她根据公式6获得了1000个LP。

LP代币金额=sqrt（100*10000）-0.000000000001=1000lp份额。假设在创建池之后发生了9个事务，如下所示——N表示创建池之后的每个期间。

考虑以下事务类：精确输出：当用户想要以任何价格购买ETH时。精确输出：当用户想要购买一个具有任意数量ETH的Dai时。精确输入：当用户想要花费一个精确的ETH数量来购买一个等价的Dai时。精确输入：当一个用户想要花费一个精确的Dai数来购买一个等价的ETH时。

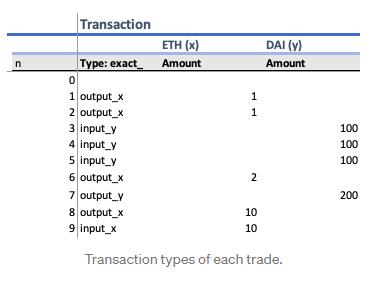
1000000的乘积常数（k）是上述交易定价机制的主要指导。它计算对池的每一方的影响应该是什么，这样就可以进行交易，并且可以保持产品常量，而不考虑成本。现在让我们计算事务对池的每一方的影响。

让我们找出n=1时的事务

初始池余额=100 ETH和10000 daiu产品=100*10000=1000000

交易类：精确输出 X→交易员希望准确购买ETH（因此他将从ETH购买）流动性从池中删除一个ETH。

新的ETH池=100-1=99 ETH→既然我们有了新的ETH池余额，那么新的Dai池余额是多少，因为池中会有大量的Dai代币？
新Dai流动性池=常数产品/新ETH池余额=1000000/99=10101.01。
根据池中Dai的流入，我们可以假设以下公式。

ETH价格=（10101.01-10000）/1=101.01→因此在n=1的交易中，交易员购买ETH的价格为101.01。
最终池余额：99 ETH和10.101.01 Dai。
我们可以在下表中看到Uniswap中的AMM，考虑到1000000的常数积和交易后的新池余额。我们还可以直观地看到每笔交易的价格和0.3%的费用。

在
事务之后，最终池概要文件是：

现在假设Tom（user10）想在n=10时增加一个ETH的流动性。由于AMM要求LPS在每一方提供一对具有相同值的代币，Tom必须提供相同数量的Dai，其值为1ETH。价格取自公式5。

所以汤姆必须提供ETH。
DAI_uuuuuuuuuamount_uuuuuuuuprovide=1*（10529/95）=110.87 DAI
因为新的流动性提供者进入池，在新的LP进入池之前需要更新交易定价的常量，新的k=96*10640=1021，170元刚好在Tom之后，另外7个LP在池中提供流动性。根据AMM提供的定价公式5，根据公式7得出相应的LP股份，如下所示。

让我们考虑下面给出的信息，以便于分析非**性损失。
汤姆进入游泳池时的初始位置是：1ETH和110.87dai。
Tom（user10_u1;Add_1ETH）决定在n=17之后随时从池中移除他们的代币。
Tom在池中的LP是Tom LP token/total uLP uuuTOKENS=10.53/1284.30=0.008199=0.82%。
在n=17之后，没有额外的流动性提供者进入池，只有交易发生。
由于以太：戴池的交易量非常大。我们可以认为Uniswap的定价机制反映了市场的真实定价，因为套利者会利用套利机会不断修正价格。
时间段（n）表示AMM中价格更新的每个时间段。
让我们比较一下当他把资产放进钱包并从池中提取流动性时，他的资本的价格更新。

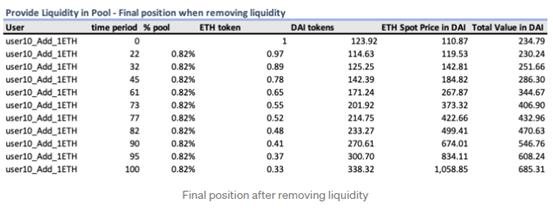
现在让我们比较以上每种情况。

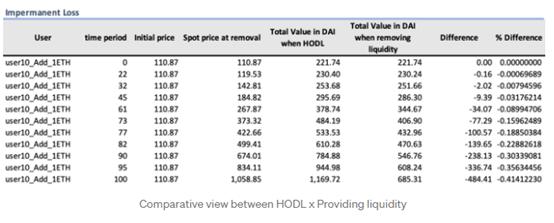
将pintail blog中的无区间损失公式应用到这个例子中，我们得到：

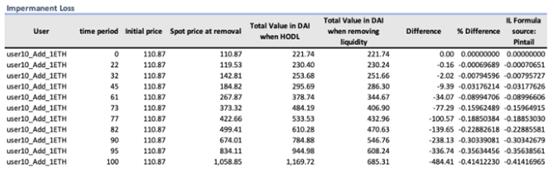
从上述模拟中，我们可以得出结论，与在钱包中持有代币相比，在提供流动性方面确实存在损失。当池中的余额发生变化，并且每个代币的价格随着池中事务的更新而变化时，就会发生这种情况。
需要强调的是，LP提供商可以将其LP从池中移除。在这种情况下，Tom在决定消除流动性的那一刻去除了当前资金池的0.8%。此时此刻，Tom想要移除流动性池，与增加流动性池相比，流动性池可能发生了变化。他的最终价格与最初的价格不同。
通过绘制价格变化图也可以观察到这种现象。

成本影响
Uniswap根据LP在池中的参与情况，将所有事务的0.3%分配给LP。因此，池中的事务越多，LPS获得的被动收入就越多。每个LP根据其在池中的比例进行分配，如上所述。
我们可以看到，Uniswap的AMM的功能是维持两个流动性池的乘积，这叫做常数，乘积与交易前的乘积（不包括费用）相同，所以有一个非**性的损失——我们可以说AMM是一个追溯的价格措施，确保双方的价值权重相同（50%） / 50%).
需要强调的是，Uniswap中的代币价格会随着交易池中的交易而更新，这在很大程度上取决于套利者在将Uniswap价格与其他交易所进行比较时发现有利可图的套利机会的能力。因此，可以说Uniswap的AMM定价完全由池中的事务决定。尽管该模可能很好地适用于非波动性资产和高波动**易池，但它可能并不适用于所有类的资产。
选项呢？
期权池
在DeFi期权（例如pods期权）中，用户必须锁定*的抵押品才能铸造期权代币。期权代币代表了买方的权利和卖方的义务。然而，由于卖方在早期阶段锁定了抵押品，因此没有什么可执行的，并且智能合约控制了卖方的义务。在
被转换成一个选项后，用户可以选择出售它或为池提供流动性。因为Uniswap是一个去中心化的协议，任何人都可以启动一个包含任何OKEX交易所对资产的池，用户可以直接在Uniswap池中出售每个系列的期权代币。
a）假设期权市场是**流动性的，AMM的价格是正确的，通过纯粹的套利能力代表了一个公平和**的价格。
或
b）仲裁池价格。如果池错误地定价的选择，它有机会缩小差距。
不幸的是，DeFi刚刚开始，所以有选择。这意味着DeFi期权市场可能无法随时修改Uniswap的价格。这意味着，如果一个资金池长期不交易，将有很大的套利机会。虽然这可能对交易者有利，但对流动性提供者可能不是那么好。
但是你怎么知道期权的价格是错误的呢？
期权定价在传统金融学中有几种定价模，其中最**的一种叫Black-Scholes。布莱克-斯科尔斯公式如下：

Black-Scholes是期权合约定价的数学模。该模的一个假设是，资产的波动性在期权期限内保持不变（这不适用-尤其是在加密货币中）。该公式仅适用于欧式期权（以及非股息资产的美式看涨期权）。
所有方法都试图在一定程度上计算出期权到期的概率，如果到期，则当前价值是多少。为了计算这样一个理论价格，笔者考虑了标的资产的现货价格、到期日、隐含波动率、无风险利率和行权价格。
期权的到期时间是期权的时间价值，也是影响Black-Scholes模定价的重要因素。
期权越接近到期日，其内在价值就越有扩大的趋势。也就是说，当期权接近到期日时，如果期权在价格范围内，其价值就会越高，因为期权被行使并获利的概率非常高，这使得期权定价更为昂贵。当期权远离到期日时，同样的逻辑也会发生：期权被执行的概率非常低，这意味着它的价值接近于零。你可以在下面看到更多关于这个概念的细节：

到期时，期权价格要么在价格内，要么在价格外。在大多数情况下，期权最终是定价的，因此期权的价值在到期时为零。
这意味着，如果用户向期权池提供流动性，并且最终超出价格，则用户可以提取更大比例的期权代币。到那时，选项标记的值可能为零。他们对quot;货币没有选择权，也没有抵押品可供提取。在考虑非**性损失时，在这种情况下，我们必须考虑交易对中的一项资产在到期时没有价值。
如果这些因素不能输入到Uniswap的定价中，它的期权价格是多少？
通用AMM期权交易
每个交易者将以他认为合适的方式处理这些公式。但大多数的期权定价方法都是综合考虑了影响期权价格的各种因素的。交易者可能会找到套利机会，但流动性提供者最终可能会损失，因为他们将资产分配给可能定价错误的交易。因此，使用Uniswap这样的模来定价期权可能不是流动性提供者的**选择。