ZKSwap 团队深入解读零知识证明算法之 Zk-STARK （四）——FRI 协议

撰文：ZKSwap 小白

前言

终于到了“零知识证明算法值 Zk-stark”系列的收尾。在前面的三篇文章里，我们依次介绍了 zk-stark 算法的整体结构、算 法的第一部分：Arithmetization、算法的第二部分：Low Degree Testing。相信通过这几篇的阅读，大家能对 zk-stark 算**廓有了个整体的认知；在阅读的过程中，你可能会对文章中的某些语句或者图片的正确性发出疑问（确实有些内容需要更具体的介绍和说明，否则会产生误解），欢迎在社区留言交流。

在第三篇文章，我们已经讲到，为了确保证明者返回的满足多项式等式相等的值确实是基于有效的多项式计算得到，我们需要对多项式进行 LDT 测试；同时为了使验证者的复杂度达到**，我们把原始多项式进行变换，变换后，证明者要证明的多项式仅仅是原始多项式的一半，不断重复这一过程，一直到多项式的度可以直接判断为止。这其实就是 FRI 协议的核心思想，下面，让我们来详细介绍 FRI 协议的过程。

FRI 协议

也许，我们应该先说一下 FRI 协议是什么？FRI，即 Fast RS IOPP，全称 Fast Reed-Solomen Interactive 预言机 Proofs of Proximity，是一种更有效的 proximiary 测试方法，测试一个点的集合大部分是在一个度小于某个值的多项式上，能达到线性级的证明复杂度和对数级的验证复杂度。在我们正式介绍 FRI 协议之前，我们先看一个简单的场景。

• 在有限域 F 上，存在一个乘法群 L0，群的阶为 2^n；
• 这时，证明者声称码字 f0:L0–gt;F 是满足 RS[F,L0,ρ] 编码参数的一个码字，即 f0 的大部分点在一个度 dlt;ρ*2^n 的多项式上 P(x) 上，这里 ρ=2^(-R)；

因此，当 f0=P 时，根据 IFFT 原理，存在 P1、P2 且 deg(P1、P2) lt; 1/2ρ2^n，满足：

f0(x) = P(x) = P1(x^2) + x * P2(x^2) (1)

令 Q(x, y) = P1(y) + x * P2(y)，可以看出 Q(x, y) 关于 x 的度 d lt; 2；关于 y 的度 d lt; 1/2ρ2^n；此时，验证者随机选取一个值 x0 发送给证明者，然后令

f1(y) = Q(x0, y) = P1(y) + x0 * P2(y) (2)

对于 f1(y)，y=x^2，由于 x 取值范围是群 1 里的元素，因此 x^(2^n) = 1 ==gt; (x^2)(2^(n-1)) = 1 ==gt; y(2^(n-1)) = 1。令 y 的作用域为群 L1，则 L1 有以下属性：

• 群的阶为 2^(n-1);
• 群 L1 的每个元素对应群 L0 的两个元素，即群 L1 的任意 y，群 L0 都有两个 x 和 (-x)mod F，满足 x^2 mod F = y AMPLAMPL (-x)^2mod F = y；

因此，问题就转化为了证明 f1(y) 的度 d lt; 1/2ρ2^n。同时也要保证函数 f1 和 f0 的一致性，流程可分为以下几个步骤：

• 验证者分别从群 L1 和群 L0 选取三个点 y,s0,s1 满足 s0!=s1 AMPLAMPL s0^2 = s1^2 = y
• 证明者返回 f0(s0),f0(s1),f1(y) 三个值
• 验证者根据 f0(s0),f0(s1) 插值出一个关于 x 的 dlt;2 的多项式 g(x)
• 验证者验证 g(s0) = f1(y)，不相等，则失败

可靠性分析：如果函数 f1 不是由函数 f0 转换而来，那么公式 (1) 的多项式 P1(x^2) 和 P2(x^2) 和公式 (2) 的多项式 P1(y) 和 P2(y) 互不相等。考虑到多项式的度 d lt; 1/2ρ2^n，变量的取值范围为 2^(n-1)，那么在这个范围内随机选取一个值，多项式相等的概率为 1/2ρ2^n / 2^(n-1) = ρ。ρ 为 coderates，如果 ρ = 2^（-8），那么一次校验成功的概率仅仅为 1/256。如果经过多次验证，那么作恶成功的概率就无线接近于 0。

以上可知，对函数 f1 重复上述的过程，直到 fr 变成一个可以直接校验的度，就完成了整个测试验证过程。

下面，我们看一下 FRI 协议的具体内容，如图 1 所示：

FRI 协议分为两个阶段：Commit 阶段和 Query 阶段。从前面简单的场景可以看出，一次简单的循环，需要 :

1. 验证者发送随机数 x0

2. 后证明者生成新函数 f1

3. 进行一致性校验

FRI 协议把每一循环前 2 步归类到 Commit 阶段，把第 3 步归类到了 Query 阶段。即在 Commit 阶段，生成所有的函数 f0~fr，r 为循环的次数，然后在 Query 阶段，统一校验。

下面，先分别介绍 Commit 和 Query 协议里各参数和各个步骤的意义，然后总结一下相关的流程。

Commit： Common input

• R RS 编码比率
• i 循环次数索引，取值 {0~r}
• r 循环次数 取值 k0-R/η
• η 空间映射参数 x–gt;x^(2^η)
• L0 群的阶 2^k0
• RS[F,Li,ρ] 编码参数 [ 有限域，作用域，编码比率 ]
• q0(x) = x^(2^η)（实际实现的定义，和图中不一致），L(i+1) = q0(Li)，表示群 Li 到群 L(i+1) 的 2^η –gt; 1 映射

Prover input

• fi 第 i 次循环的函数输入
• Li 第 i 次循环的群，阶位 2^(n-i)
• RSi fi 对应的编码参数

LOOP i lt;= r

• 1

  • xi 验证者发送的随机数

• 2

  • Sy 群 L(i+1) 的每一个元素对应于群 Li 的元素的集合
  • f(i+1)(y) 计算 f(i+1) 在群 L(i+1) 上的所有取值

• 3 i==r

  • 定义 fr 第 2 步的输出
  • 插值出 P(x)
  • d 是多项式 P(x) 的度
  • 保存 d+1 个多项式 P(x) 的系数 a0~ad
  • Commit 阶段终止

• 4 i lt; r

  • 定义 f(i+1) 按照第 2 步的计算方式
  • 保存 f(i+1) 的值，在群 L(i+1)
  • 进入下一步循环

Query verifier input

• R /η /Li /RSi /xi /fi /P(x) 见 Commit
• l query 次数

重构 fr

• 获取 a0~ad，重构 P`(x)
• 计算 P`(x) 在群 Lr 上的所有取值，并赋值给 fr，注 fr 满足 RSr

repeat l times

• i = {0~r-1}

  • Si 满足 s(i+1) = q0(x) 的 x 的集合

• i = {0~r-1}

  • 在 Si 上，插值出 Pi(x)

• round consistency check i = {0~r-1}

  • f(i+1)(s(i+1)) = Pi(xi)

• 都成功，则验证通过

下面，以 η = 1 （即，q0(x) = x^2）为例，FRI 协议的两个阶段的过程如图 2 所示：

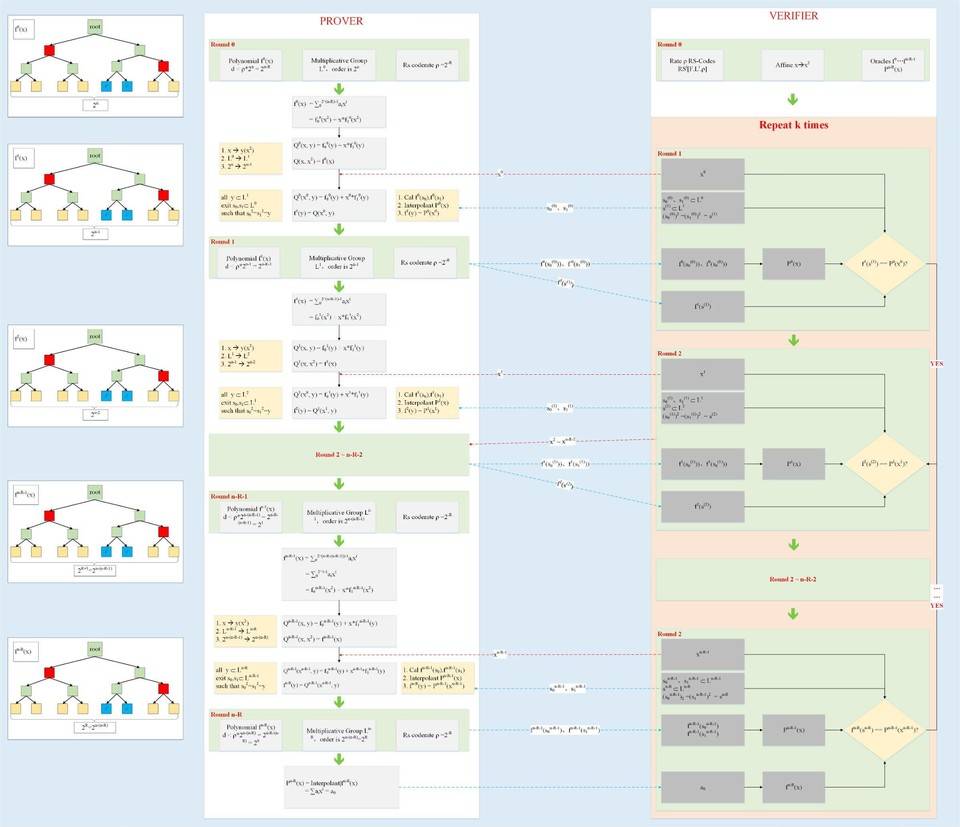
由以上流程可以看出：

• 针对每一轮的一致性的校验，确保了原始多项式 f0 的确满足 d lt; ρ*2^n
• 上述协议重复 l 次，可以大大降低作恶者成功的概率

总结

以上就是 FRI 协议的具体过程，可以看出，验证复杂度满足对数关系 r = Log2(ρ2^n)。算法保证了，当且仅当原始多项式 f0 是小于 ρ2^n 时，所有的 round consistency 校验才会通过。真正的实现可能略有差别，具体的可以参考 DEEP-FRI 论文，相对于 FRI，DEEP-FRI 在保持证明和验证的**复杂度的同时，提高了系统的可靠性。 结合本系列的前三篇的文章，总结 ZK-STARK 的算法如下：

1. 算法分为两部分：算术化和 LDT

2. 算术化把问题转换位多项式相等以及多项式的 LDT 问题

3. LDT 阶段使用 FRI 协议，保证线性级的证明复杂度和对数级的验证复杂度

4. 零知识属性保证验证者不能访问轨迹多项式里的点，轨迹多项式里保存着隐私值

5. 同时为了保证零知识属性，需要对轨迹多项式附加数行随机值，由验证者和证明者协商确定

6. 整个过程，不需要第三方的 CRS

7. 整个过程，不依赖任何数学难题

附录
官方 FRI 的简单介绍 https://medium.com/starkware/low-degree-testing-f7614f5172db

FRI paper https://eccc.weizmann.ac.il/report/2017/134/

DEEP-FRI paper https://arxiv.org/abs/1903.12243https://en.***.org/wiki/Reed–Solomon_error_correction

来源链接：zks.org