ZKSwap 团队理解零知识证明算法之 Bulletproofs：Range Proof 2

撰文：ZKSwap 江小白

前言

在本系列的 第一篇文章 中，我们介绍了 Bulletproofs 在 Range proof 上的应用，当 prove r 想要证明 v 值在范围 [0, 2n-1] 内时，他需要发送 2n+7 个元素。然而，这种 O(n) 级的 CC 并不是我们想要的，希望能寻找一种方法可以把 CC 降低到 O(log(n) 级。

所以，本篇我们就主要介绍这个优化过程，主要分为两部分：

1. 以简单的场景去阐述这个优化过程

2. 把第一篇的 Range proof 结果嵌入到优化过程

注：第一篇文章由于格式的原因，公式显示会有误差，向量的特殊标记也没有显示出来，因此本篇将以图片的形式展示整个过程；另外，本文**也附上了第一篇文章的图，帮助大家理解 ^_^

Improved Range proof—- A simple example 1. 预备知识

2. 一个简单的场景

3. 复杂度优化到 O(log(n))

上图是一张基于上述过程的交互协议

有几点需要说明：

1. 图的右半部分分为两个部分

a. 黄色部分为文章前面部分讲述的过程。这又分为三个部分：

i. 初始化：省略了 P 的计算和交互的过程，我们假定开始此证明协议前，验证者已经有了一些基本的信息。这并不严谨，仅仅是为了清晰的表示后面的交互过程

ii. LOOP ：一个不断迭代的过程，每次迭代，会 :

• 产生一对 (Li, Ri)，

• 所有向量长度减半

• Verifier 计算 P i /g i / h i`

iii. End：**一步，向量 a, b 已减半成常量 a, b

b. 绿色部分为黄色部分的进一步优化，优化思想主要是多次幂乘操作缩减成单词幂乘操作，具体的是：

i. 上述 LOOP 中的第 3 步，延迟到**一部一次性计算

A real Rang proof

回顾第一篇文章，我们知道，当我们要证明 v 属于 [ 0, 2n-1 ] 时，验证者最终要验证：

对关系式做个变换：

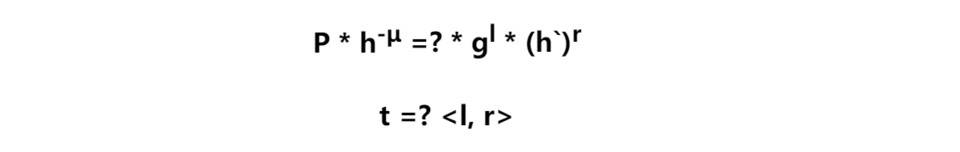
因此，prover 是要证明有向量 l，r 满足关系：

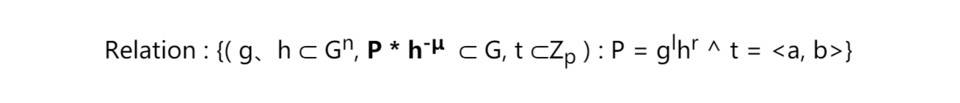
基于此关系，使用上述协议，就可以使 range proof 的交互复杂度降低到对数级。现在，是不是找到点内味了？

总结

本篇文章主要讲到了，BulletProof 是如何把 Range proof 的 CC 降低到 O (log(n))，并且介绍了更近一步的优化。结合第一篇文章，相信你已经对基于 Bulletproofs 的 Range proof 原理有了整体的了解，在本系列的第三篇文章中，将给大家分享 Range proof 的工程上实现细节。

附录

1. Bulletproofs 论文：https://ieeexplore.ieee.org/stamp/stamp.p?tp=AMPLarnumber=8418611

2. 附一张图，方便大家理解上一篇文章

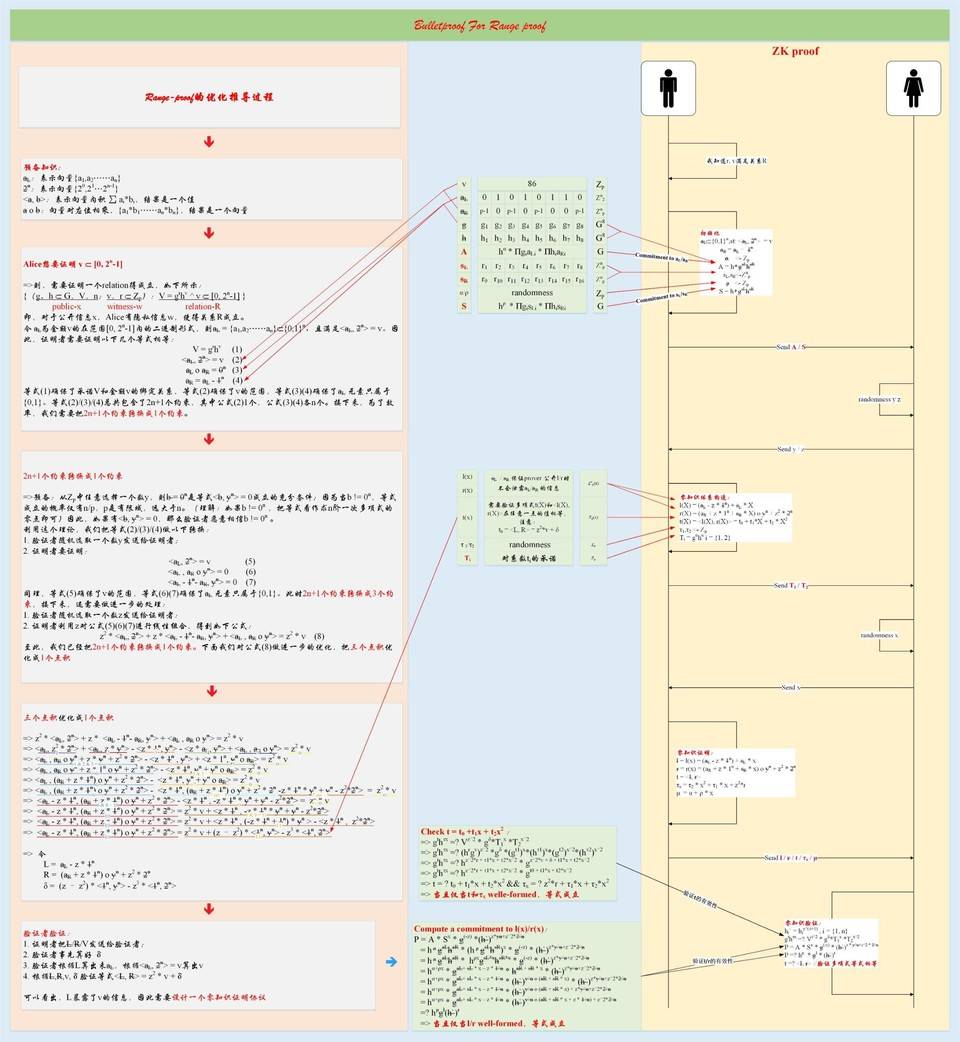
来源链接：zks.org