硬核 | 技术解析热门零知识证明方案 Groth16

Groth16 是实践中使用最广泛的 zkSNARK，其 Verifier 性能快，证明字符串短，缺点是需要对每个电路都执行一次可信初始化。

原文标题：《一起了解最热门的 zkSNARK 方案——零知识证明引论（三）》
撰文：Cyte

在之前的文章中，我们介绍了零知识证明的 基础概念 以及构造 zkSNARK 的 基本思想和方法。从本文开始，我们将逐一介绍目前最热门的 zkSNARK 方案。文章旨在让读者理解这些方案的基本原理。为了方便叙述并容易理解，在叙述方案时，我们会做一些简化处理，重在传达方案的核心思想。

本文介绍的是 Groth16 方案。Groth16 方案，顾名思义，就是 Groth 在 2016 年发表的一篇论文 [Gro16] 中提出的方案。目前为止，Groth16 是在实践中使用最广泛的 zkSNARK (没有之一)。特别一提的，Zcash 目前使用的 zkSNARK 方案就是 Groth16。从性能上，Groth16 的 Verifier 性能是所有 zkSNARK 中最快的，其证明字符串也是最短的。

而 Groth16 的**缺点就是它需要对每个电路都执行一次可信初始化。

在介绍 Groth16 之前，简单回顾一下 zkSNARK 所要解决的问题。我们称这个问题为「计算验证问题」。

计算验证问题

任何计算都可以描述为一个算术电路。一个算术电路可以对数字进行算术运算。电路由加法门、乘法门以及一些常数门组成，如下图所示：

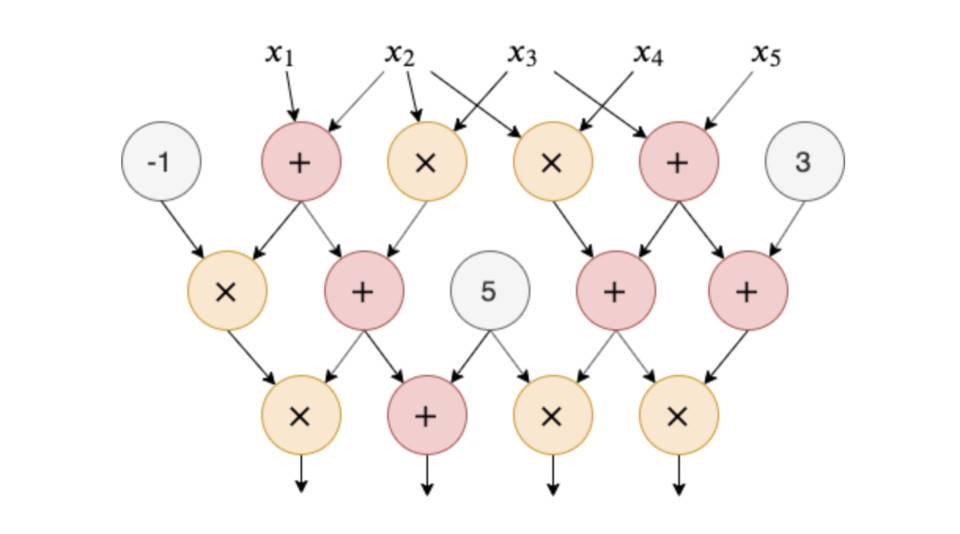
这个例子中的电路包含了 15 个门。这个电路所描述的计算过程需要输入五个数字 x1 到 x5，输出四个数字。

给定一组输入的数字，需要把这个电路中的每个门都计算一遍，才能计算出这个电路的输出。在这个例子中，如果输入是 (1,2,3,4,5) ，则电路的输出为 (-27,14,80,171)，如下图所示：

计算验证问题是指，如果一个验证者——不妨叫做 Verifier——只拿到了电路的一组输入和输出，如这个例子中的 (1,2,3,4,5) 和 (-27,14,80,171) ，它该如何验证这是一对合法的输入和输出呢？最简单粗暴的方法就是把这个输入重新扔进电路算一遍。如果电路很大的话，这个验证方法**的缺点就是效率问题。

有些场景下，效率还不是唯一的问题。例如，输入可能包含 Verifier 不能知道的秘密信息。假设上例中的 (3,4,5) 是秘密输入，Verifier 只能看到 (1,2) ，如下图所示。此时 Verifier 要验证的问题就变成了「是否存在 (?,?,?) 使得电路在输入 (1,2,?,?,?) 的时候的输出是 (-27,14,80,171) 」。这个场景下，即使是简单粗暴的重新计算也不再可行。

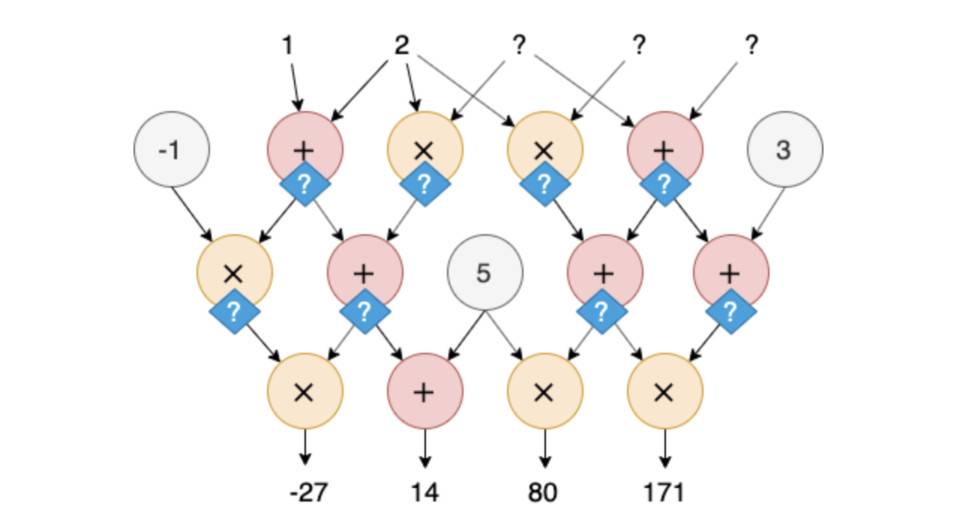
一句话概括计算验证问题：Verifier 能否在不知道秘密输入的情况下，高效地验证计算结果？

从电路到 R1CS 问题

一个 zkSNARK 就是对上述问题的一个解决方案。使用 zkSNARK，一个证明者，叫做 Prover，可以为计算过程生成一个简短的证明字符串。Verifier 读取这个字符串，就可以判断给定的公开输入和输出是否合法。

Groth16 是众多 zkSNARK 构造方案中的一种。接下来，我们介绍 Groth16 是怎么解决计算验证问题的。

首先，我们重新审视一下 Verifier 的任务：我们只知道电路的前两个输入是 (1,2)，我们的目标是要判断是否存在一组合法的秘密输入，使得电路的输出是 (-27,14,80,171)。如果我们换个角度看这个问题，它其实可以描述为：给一个电路，上面有些空格可以填数字，有些空格已经填上了数字，请问是否存在一种填法，能够同时满足每个门的逻辑？

从这个新的角度，计算验证问题被转换成了一个类似于数独那样的填数字游戏：有一些空格，一部分已经填上，请你填上另外一些空格，满足一些限制条件。

然后，我们为每一个要满足的条件列一个方程。这里，每个要满足的条件其实就是一个门的逻辑：加法门的输出等于两个输入之和，乘法门的输出等于两个输入之积。于是，原来的填空游戏就变成了一个多元方程组。上述例子转化得到的方程组如下：

**，我们对这个方程做一些整理，使得它能够写成矩阵和向量的形式，更加整齐和简洁。我们把每个方程都写成 * = * x * 的模式。尽管并不是所有方程中都有乘法，但我们可以给没有乘法的式子乘上一个 。于是方程组变成了下面这个样子：

把所有方程合到一起，就得到了原方程组的矩阵表示

我们把最终得到的这个矩阵向量方程叫做一个 Rank-1 Constraint System (R1CS)。

总结一下，这一节中我们把计算验证问题转化成了数学问题 R1CS。

在计算验证问题中，Verifier 知道一个电路，拿到公开部分的输入，以及电路的输出，判断它们是否合法。

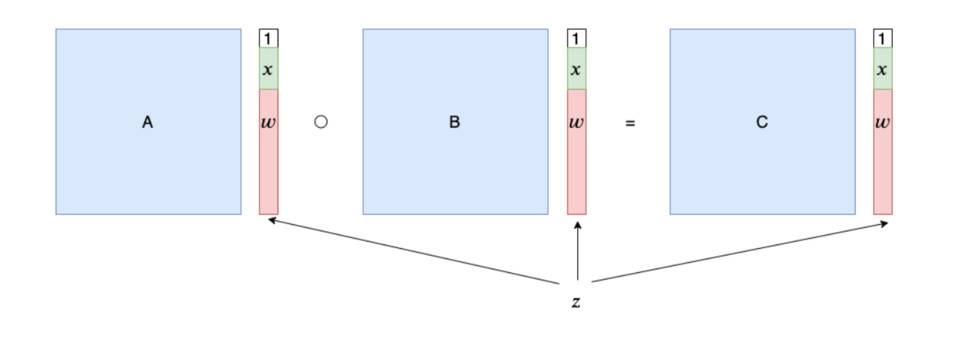
从 R1CS 问题到 QAP 问题

在零知识证明领域，R1CS 基本上就是电路的代名词。许多 zkSNARK 把 R1CS 问题作为目标问题。不过，大部分 zkSNARK 不会直接对 R1CS 下手，而是把 R1CS 问题继续转化，得到一个等价的多项式问题，再对这个多项式问题设计证明方案。Groth16 也不例外。不同的 zkSNARK 选择的多项式问题各不相同，Groth16 选择的是一个叫做 Quadratic Arithmetic Programming (QAP)的问题。

这一节中介绍一下怎样把 R1CS 问题转化为等价的 QAP 问题。

然后，我们把这些列向量换成多项式，使得多项式方程和原先的向量方程等价。

把向量转化成多项式的一种方式是使用多项式插值。

多项式插值

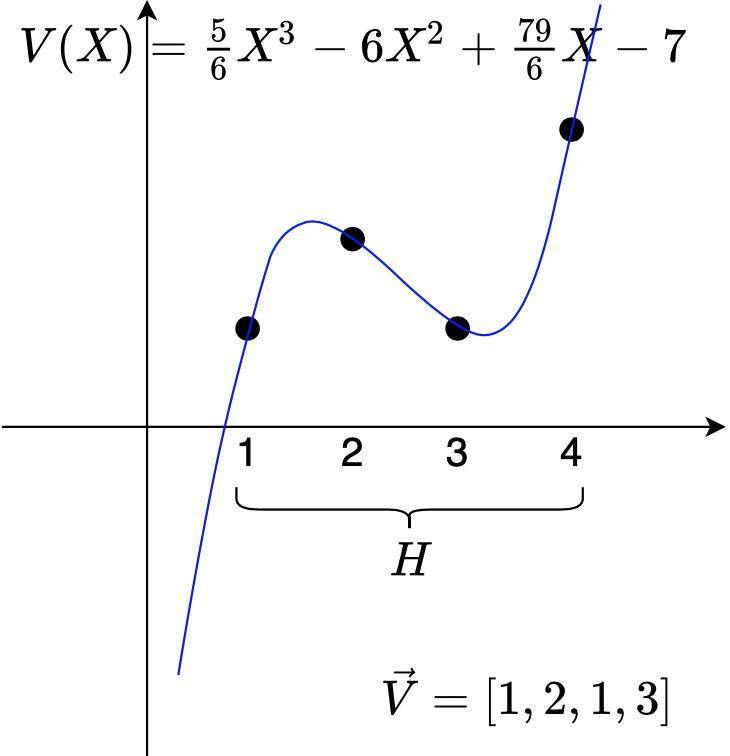
QAP 问题

现在，我们直接把 R1CS 矩阵中的列向量换成它们的多项式插值，得到的结果如下图所示。

我们用一个表格总结一下上文中提到的所有问题。

为什么要越搞越复杂，把电路问题转化为 QAP 问题呢？一个简单的回答：就是为了引入多项式！多项式是一个强大的工具。多项式的作用，可以理解为一个「杠杆」，或者叫「误差放大器」。如果我们要检查两个长度为 10000 的向量是否相等，一定需要检查 10000 次，哪怕检查过了 9999 个点都是一样的，也不能保证**一点是相同的。而两个 10000 次的多项式，哪怕非常接近，比如说它们的系数有 9999 个都相同，或者它们在 这些点上的取值都相等，但只要有一个点不同，这两个多项式就截然不同。这意味着，如果在一个很大的范围内，例如 到 当中均匀随机选一个点，两个不同的多项式在这个点上相等的机会只有 。检查两个多项式是否相等，比检查同样规模的向量要快得多，这几乎是所有 zkSNARK 提高 Verifier 效率的根本原理。

为 QAP 问题构造 zkSNARK

QAP 问题就是 Groth16 要用来构造 zkSNARK 的最终问题了。不过，在解释 Groth16 的构造细节之前，我们先准备一些工具。

准备工具

我们假设读者对椭圆曲线群的基本特性和应用有所了解，并采用加法群的记号来描述椭圆曲线群中的点和运算。椭圆曲线群中的元素可以用来表示多项式，并限制 Prover 必须使用给定的多项式来进行线性组合。这正是 QAP 所需要用到的特性。

我们看一下椭圆曲线是怎么用来表示多项式的。

KoE 假设

然而，上述直觉并不能从离散对数假设严格地证明而来。所以，只能把它作为一个新的安全性假设来用。这个假设就叫做 Knowledge-of-Exponent (KoE) 假设。

KoE 假设怎样应用到 QAP 问题上呢？那就是，KoE 允许我们使用椭圆曲线点来表示多项式，并且迫使 Prover 只能从已知的多项式线性组合产生新的多项式。

不过，到目前为止，我们忽略了两个关键问题：

关于第二个问题，一个解决方法就是双线性配对。

双线性配对

现在，我们已经准备好了工具：KoE 假设和双线性配对。接下来，我们就介绍 Groth16 是如何为 QAP 问题构造 zkSNARK 的。

Groth16 方案

Setup

Prove

Verify

解析

我们简单解释一下上述构造为什么能够工作。至于它为什么是安全的，请感兴趣的读者参阅 [Gro16] 原文。

当然，Verifier 的验证式中还包含了许多其他项，但在 Groth 的精心设计下，它们都消掉了。感兴趣的可以自行验证。

小结

本文中，我们解释了 Groth16 这个 zkSNARK 方案的构造原理。我们从算术电路开始，介绍了怎样将计算验证问题转化为 R1CS 问题以及 QAP 问题。然后我们解释了怎样使用 Groth16 方案来证明知道一个 QAP 问题的解。Groth16 方案使用了 KoE 假设以及双线性配对。它的缺点是需要可信第三方进行初始化，而且初始化过程需要对每个电路进行一次。与此同时，Groth16 享有**效的 Verifier 算法以及最短的证明字符串，使得 Groth16 成为至今仍然应用最广的 zkSNARK 方案。

参考资料

[Gro16] Jen Groth. On the Size of Pairing-based Non-interactive Argument. 2016.