核心技术分析热零知识证明方案groth16

Groth16是实践中使用最广泛的zksnark。它的验证器具有速度快、验证字符串短的特点。缺点是它需要为每个电路执行可信初始化。

原题：了解***的zksnark方案——零知识证明简介（3）
作者：cyte

在前一篇文章中，我们介绍了零知识证明的基本概念以及构造zksnark的基本思想和方法。从本文开始，我们将逐一介绍***的zksnark方案。本文旨在使读者了解这些方案的基本原理。为了便于描述和理解，我们将简化方案的描述，重点传达方案的核心思想。

本文介绍了groth16的设计方案。顾名思义，Groth16方案是groth在2016年发表的一篇论文[gro16]中提出的方案。到目前为止，groth16是实践中使用最广泛的zksnarks之一。特别是，zcash目前使用的zksnark方案是groth16。在性能方面，groth16的验证器性能是所有zksnarks中最快的，其证明字符串也是最短的。

groth16**的缺点是它需要为每个电路执行可信初始化。

在介绍groth16之前，让我们简要回顾一下zksnark必须解决的问题。我们称这个问题为“计算验证问题”。

计算验证问题

任何计算都可以用算术电路来描述。算术电路可以对数字进行算术运算。电路由加法门、乘法门和一些常数门组成，如下图所示

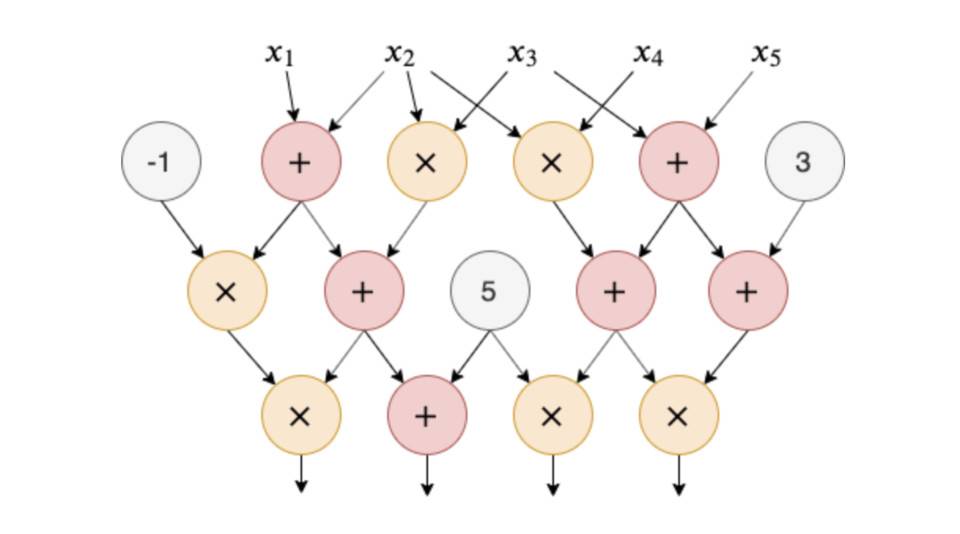
本例中的电路包含15个门。此电路中描述的计算过程需要5个输入数字X1到X5和4个输出数字。

给定一组输入数字，在计算电路的输出之前，需要计算电路中的每个门。在本例中，如果输入为（1,2,3,4,5），则电路的输出为（-27,1480171），如下图所示：

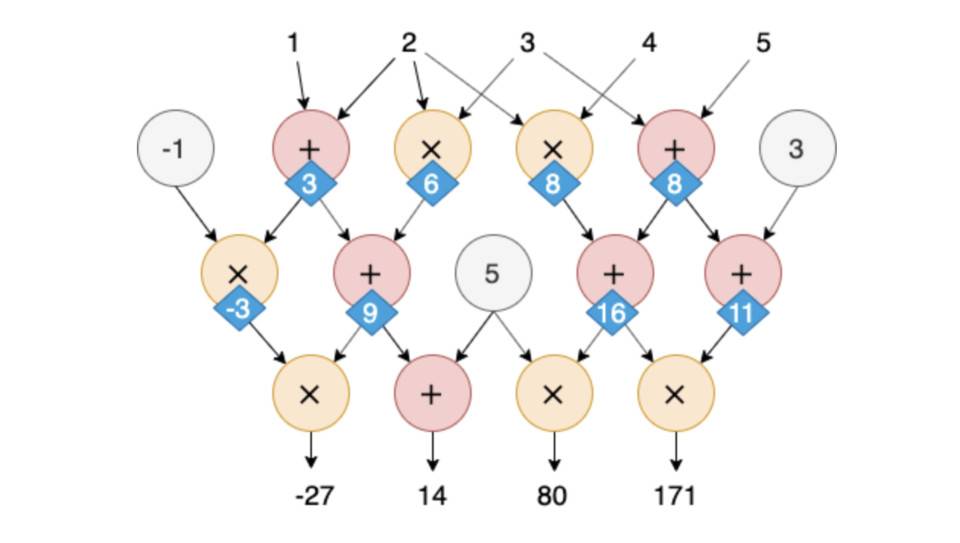
计算验证的问题是，如果一个验证器——或者它可能被称为验证器——只获得电路的一组输入和输出，例如本例中的（1,2,3,4,5）和（-27,1480171），它如何验证它是一对合法的输入和输出？最简单和最粗糙的方法是将这个输入返回到电路中并进行计算。如果电路很大，这种验证方法**的缺点就是效率。

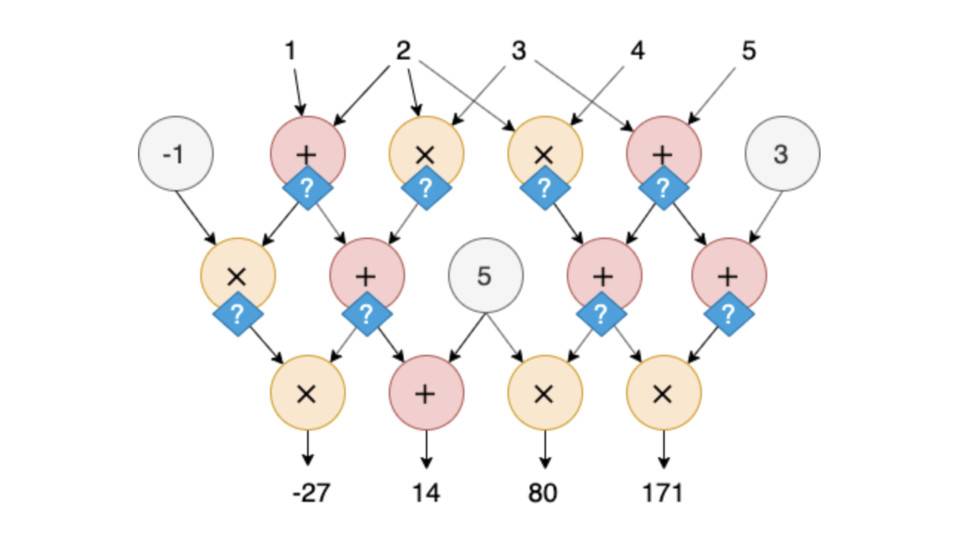
在某些情况下，效率并不是唯一的问题。例如，输入可能包含验证者不能知道的秘密信息。假设上例中的（3,4,5）是秘密输入，验证者只能看到（1,2），如下图所示。这时，验证者要验证的问题就变成了“是否存在（？）？,?,?) 使电路的输出在输入端（1，2，？,?,?) 是（-27,1480171）”。在这种情况下，即使是简单粗略的重新计算也不再可行。

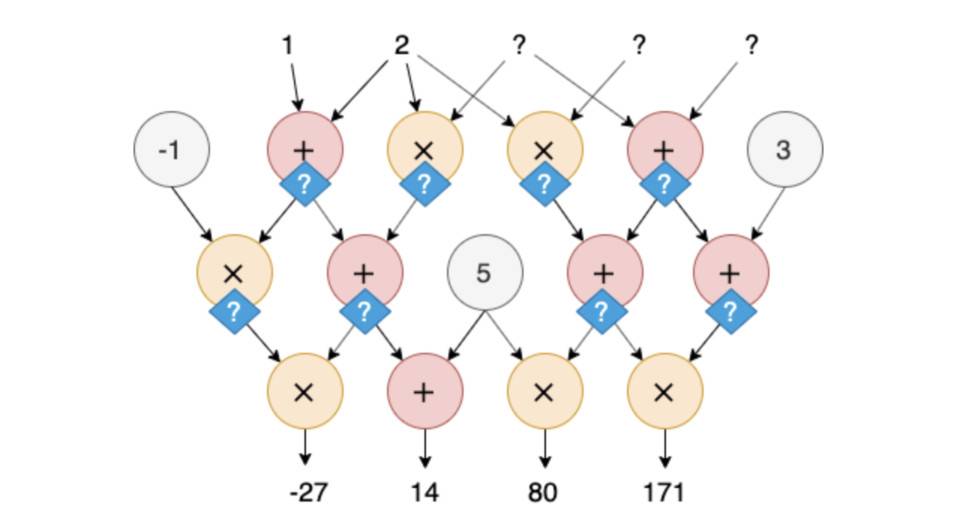
总之，计算验证问题可以概括为：验证者在不知道秘密输入的情况下能否有效地验证计算结果？

从电路到r1cs问题

zksnark是上述问题的解决方案。使用zksnark，验证程序可以为计算过程生成一个简短的验证字符串。验证器读取此字符串以确定给定的公共输入和输出是否合法。

Groth16是众多zksnark施工方案之一。接下来，让我们介绍groth16如何解决计算验证问题。

首先，我们重新审视了验证器的任务：我们只知道电路的前两个输入是（1，2）。我们的目标是确定是否有一个秘密输入的组合方法，使电路的输出是（-27，1480171）。如果我们从另一个角度来看这个问题，它可以被描述为：对于一个电路，一些空间可以用数字填充，而一些空间已经用数字填充。是否有一种填充方法可以同时满足每个门的逻辑？

从这个新的角度，计算验证问题被转化为一个类似于数独的数字填充游戏：有一些空间，其中一些已经被填充。请填写其他空格以满足某些限制。

然后，我们为每个条件建立一个方程。这里，每个需要满足的条件实际上是一个门的逻辑：加法门的输出等于两个输入的和，乘法门的输出等于两个输入的乘积。这样，原来填空的游戏就变成了一个多方程组。从上述例子得到的方程式如下：

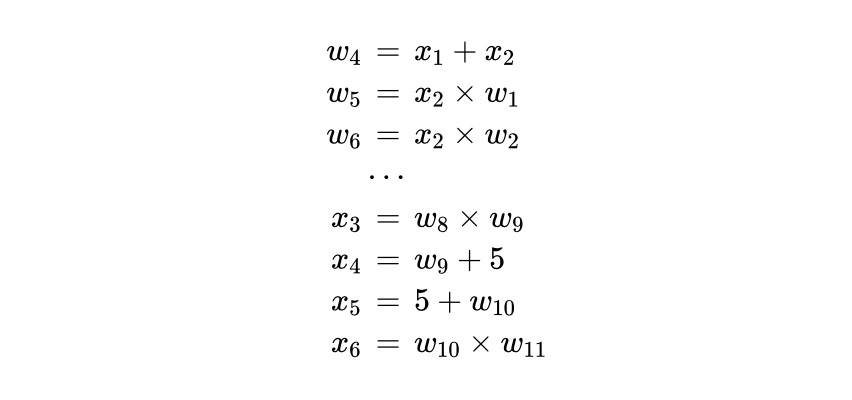
**，我们对这个方程作了一些整理，使之可以写成矩阵和向量的形式，更加简洁明了。我们把每个方程写成*=*x*的模式。虽然不是所有的方程都有乘法，但我们可以不乘法就乘法一个方程。所以方程是这样的：

将所有方程组合，得到原方程的矩阵表示

我们将得到的矩阵向量方程称为秩1约束系统（r1cs）。

总之，在本节中，我们将计算验证问题转化为一个数学问题r1cs。

在计算验证问题中，验证者知道一个电路，得到公共部分的输入和电路的输出，并判断它们是否合法。

从r1cs到QAP

在零知识证明领域，r1cs基本上是电路的同义词。许多zksnark都把r1cs问题作为目标问题。然而，大多数zksnark并不直接处理r1c。相反，他们继续将r1c转化为一个等价的多项式问题，然后为这个多项式问题设计一个证明方案。Groth16也不例外。不同的zksnarks选择不同的多项式问题。Groth16选择了一个叫做二次算术规划（QAP）的问题。

本节介绍如何将r1cs问题转换为等效的QAP问题。

然后，将这些列向量转化为多项式，使多项式方程等价于原向量方程。

将向量转化为多项式的一种方法是使用多项式插值。

多项式插值

QAP问题

现在，我们直接将r1cs矩阵中的列向量替换为它们的多项式插值，结果如下图所示。

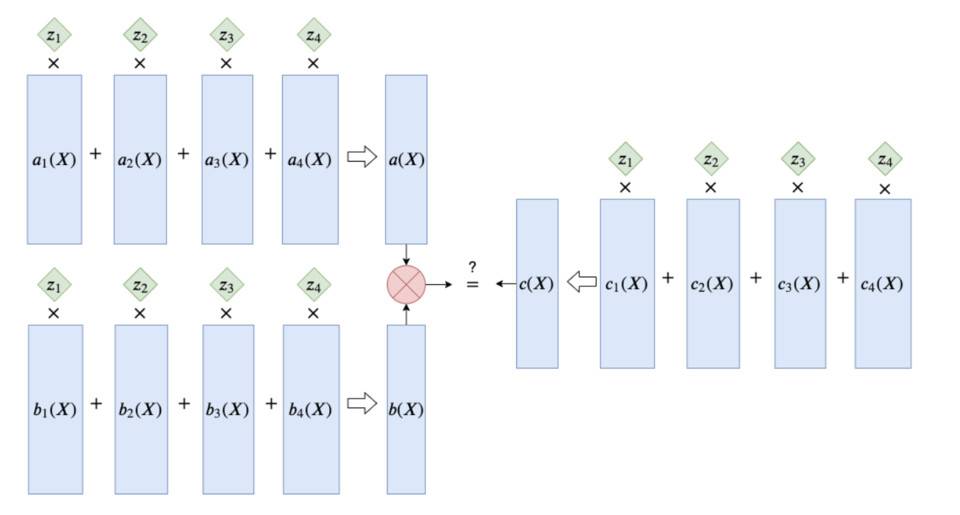
让我们把上面提到的所有问题归纳成一张表。

为什么我们要把电路问题变成QAP问题？一个简单的答案：介绍多项式！多项式是一个强大的工具。多项式的函数可以理解为“杠杆”或“误差放大器”。如果我们要检查两个长度为10000的向量是否相等，我们必须检查10000次。即使9999点是一样的，我们也不能保证**一点是一样的。即使两个10000次的多项式非常接近，例如，它们的9999个系数是相同的，或者它们在这些点上的值是相同的，但是只要一个点不同，这两个多项式就完全不同。这意味着，如果一个点在很大范围内随机选择，例如，两个不同的多项式在这一点上只有一个相等的机会。检验两个多项式是否相等比检验相同尺度的向量要快得多。这是几乎所有zksnarks提高验证器效率的基本原理。

QAP问题zksnark的构造

QAP问题是groth16将用于构建zksnark的**一个问题。然而，在我们解释groth16的构造细节之前，让我们先准备一些工具。

准备手段

假设读者对椭圆曲线群的基本性质和应用有一定的了解，并用加法群的符号来描述椭圆曲线群中的点和运算。椭圆曲线群的元素可以用来表示多项式，证明者必须用给定的多项式进行线性组合。这正是QAP所需要的。

让我们看看椭圆曲线是如何用来表示多项式的。

KOe假说

然而，上述直觉并不能从离散对数假设中得到严格的证明。因此，它只能作为一种新的安全假设。这一假说被称为指数知识假说。

如何将kOe假说应用于QAP？也就是说，kOe允许我们使用椭圆曲线点来表示多项式，并强制证明器仅从已知多项式的线性组合中生成新的多项式。

然而，到目前为止，我们忽略了两个关键问题：

第二个问题的一个解决方案是双线性配对。

双线性对

现在我们已经准备好了工具：kOe假设和双线性配对。接下来，我们将介绍groth16如何为QAP问题构造zksnark。

Groth16溶液

安装程序

证明

验证

分析

让我们简单地解释一下为什么上面的结构是有效的。至于为什么它是安全的，请参考[gro16]的原文。

当然，验证器的验证器中还有许多其他项，但它们都被格罗斯的精心设计所消除。有兴趣的可以自我验证。

摘要

本文阐述了groth16-zksnark方案的施工原理。从算法电路出发，介绍了如何将计算验证问题转化为r1cs问题和QAP问题。然后我们解释了如何使用groth16方案来证明我们知道QAP问题的解。groth16方案采用kOe假设和双线性配对。它的缺点是需要由可信的第三方初始化，每个电路需要初始化一次。同时，groth16具有最有效的验证算法和最短的证明字符串，使groth16成为应用最广泛的zksnark方案。

标准物质

詹·格罗斯。基于配对的非交互变元的大小。2016