比特币算法演变成施诺尔签名算法是一种进步吗？

历史的车轮滚滚向前，技术的进步从未停止，一项具有里程碑意义的特殊货币协议开始了其技术升级。Schnorr签名和主根已集成到比特币核心0.21.0版本中。

比特币的未来似乎从未如此光明。现在，它有机会超越所有其他区块链，不仅通过其容量，而且通过其功能。

当采用比特币ECDSA椭圆曲线签名算法时，多重签名的交易验证过程非常繁琐。现在一个事务中所有的签名和公钥都可以合并成一个签名和公钥，这样既不可追踪又简单快捷？

事实上，在此之前，中本聪在设计比特币协议时，需要考虑签名算法的签名长度、是否开源、是否拥有专利、是否经过足够长时间的安全验证、性能等条件。当时，不仅ECDSA，而且Schnorr签名在各个方面都不亚于ECDSA，都能满足上述条件。但是，由于2008年以前的专利保护状况，可能正是这个原因，中本在设计比特币协议时没有使用签名算法，最终选择了椭圆曲线数字签名算法（ECDSA），在其他专家的建议下，也选择了一种特殊的椭圆曲线secp256k1。

10年后的2018年7月，比特币开发者皮耶特·乌伊尔（Pieter wuille）撰写了BiP Schnorr，并提出将比特币的签名算法改为Schnorr方案。虽然Schnorr和ECDSA都是使用secp236k1曲线的椭圆曲线加密算法，但由于Schnorr签名在密码学中的优势，在几乎相等安全性的基础上构造多签名事务更为方便。

在比特币中使用时，Schnorr比ECDSA有一些额外的显著优势

更安全：在随机预言机模中很容易证明Schnorr签名的安全性，但是ECDSA没有这样的证明。

无可伸缩性问题：ECDSA签名是可扩展的。第三方可以在不知道私钥的情况下直接修改现有签名，并且仍然保持签名对该事务的有效性。比特币一直存在可伸缩性攻击，这些攻击在segwit被激活之前是不固定的，前提是使用segwit事务而不是传统事务。Bip62和bip66对此进行了详细描述。

线性：Schnorr签名算法是线性的！基于这个特性，我们可以构建一个更高效、更隐私的区块链系统。使用Schnorr签名的各方可以为各自的密钥生成签名聚合。例如，如果使用n个公钥进行签名，并且使用ECDSA，则n个签名可用，并且还需要进行n次验证。如果使用Schnorr，由于其线性特性，只能保留最终的叠加签名。例如，无论输入多少个事务，同一个事务都可以叠加到一个签名中，签名可以验证一次。

Schnorr签名算法在性能、安全性、体积、可扩展性等方面几乎都优于现有的比特币签名算法ECDSA，并且Schnorr sig可以使用与ECDSA相同的椭圆曲线：secp256k1曲线，因此升级非常小。

当然，除了签名算法之外，taproot脚本语言还用于定义如何使用比特币。比特币多签名者类地址既不能公开其“多签名者”身份，又支持大量的多签名者场景（链上交易只需要一个聚合公钥和一个签名），可以减少大量的交易字节，特别是对于需要高频操作的地址。降低供应链上的交易成本可以节省大量成本。

以下是一些常见的问题和答案：

问答

Q： Schnorr签名能用于M/N多重签名吗？
A:当然。多重签名只是签名个数m/n的一种模式，与签名算法无关。

Q： Schnorr的群签名能生成或模拟m/N签名吗？
A:这不可能。如果一个组中有n个公钥，则必须有n个签名。当每个人生成一个签名时，在哈希函数中替换组公钥p。

Q： 如何衡量签名机制的安全性？
A：主要看两个方面：1。签名算法本身。椭圆曲线。目前，Schnorr和ECDSA都使用同一级别的曲线secp256k1。在签名算法本身的安全性方面，Schnorr具有比ECDSA更好的安全性证明。

关于BCH

Schnorr签名算法

早在2019年5月16日，BCH就开始了硬叉升级。升级的主要内容是Schnorr签名算法和隔离见证恢复，这是Schnorr签名升级中最期望的功能，而隔离见证恢复是一种恢复性技术，用于检索错误发送到隔离见证地址的BCH。

开发者marklundeberg用户不必生成新地址就可以开始使用Schnorr签名。升级到BCH的好处如下：

提高签名数据的有效性：

因为签名是64字节的数据，与通常的70字节相比，事务可以减少4%。此功能基本上提高了每次比特币现金交易所需签名数据的有效性（Schnorr签名将使区块链存储和带宽至少减少25%，并使BCH网络更快、更高效）。升级后，施诺尔签名给BCH带来了隐藏普通支付渠道的能力。

隐私增强：

在升级之前，很多用户会故意使用多个签名来发送交易以提高隐私，而Schnorr签名会使所有用户的签名看起来像任何其他签名，从而导致交易隐私的实质性提高。Schnorr提供的属性以及BCH开发人员和基础设施提供商添加的一些扩展（如钱包）将进一步增强隐私性和可扩展性。

打击垃圾邮件交易攻击：

在过去，有一个垃圾邮件交易攻击。攻击者想用尽可能多的交易空间来阻塞比特币。他们的方法之一是频繁地从多个来源发送事务，因此事务中包含了几十个签名。这些签名占用了大量的空间，是ECDSA签名留下的隐患。

Schnorr可以避免此类垃圾邮件交易攻击。如果每个事务只有一个签名，则块可以容纳更多事务。为了创建攻击，垃圾事务生成器必须发送更多的事务以与更多的人竞争，因此攻击成本相对较高。签名空间通常是事务的**部分，因此攻击者没有优势。

当然，我们不能只看到好的一面，我们必须缺少一切，如果我们是极端的，我们必须是消极的。特别是量子计算机的发展对区块链的安全构成了威胁。为了解决量子计算机对某些算法的攻击，NIST在2017开始了后量子密码术的标准化过程，包括ABCMICT基金会在瑞士推广的反量子签名方案，后量子加密基础上的抗量子算法之一，最短签名长度彩虹的抗量子签名方案，量子签名方案，是最有前途的。

2017年8月，刘瑾和数学家丁金泰教授在瑞士苏黎世附近的cryptovalley成立了abcmint并注册。彩虹签名是ABC数字货币的基础签名。他们的愿景是支持国际上反量子计算机破解算法的研究和应用。研究内容包括国内外数学家对算法的发现、破解和改进，以及在主流数字加密货币中适当算法的应用。

他们认为，bip340是比特币从ECDSA改为Schnorr签名的提案，采用了Schnorr签名，这是比特币的一次重大倒退。我们对计算机安全专家提出的算法选择和改进并不乐观。我们更喜欢数学家提出的算法选择和改进。Schnorr签名是一个大问题，应该用于长期的测试运行，比如litecain。

BTC应该等BCH或其他公链签下施诺尔几年。Schnorr签名的主要优点是“当有多个签名时，签名的长度最短”，缺点是“当有多个签名时，**一个人很容易被欺骗”。

从密码学的角度看，采用Schnorr签名是quot;的大胆和轻率的做法，背离了“长期安全”的基本含义。

从密码学的角度来看，Schnorr签名主要是针对多重签名的，适合多重签名的场景是中心化的、极其重要的场景，类似于核弹发射的十多个可验证程序。或下燕山核武器基地。它不应该是去中心化的场景或比特币发送场景。

简单地说：去中心化本身就是对多重签名的背离。

以下是一些简单的算法：

椭圆曲线数

签名算法（ECDSA）

椭圆曲线数字签名算法（ECDSA）是针对NIST对数字签名标准（DSS）的要求，Scott和Vanstone于1992年**提出的由Neal-Koblitz和victor-ECDSA组成的椭圆曲线密码体制（ECC）对数字签名算法（DSA）的模拟。

目前，比特币采用ECDSA椭圆曲线数字签名算法。要对消息M签名，我们需要对其进行散列，并将散列视为一个数字：z=散列（M）。我们还需要一个随机数或随机数K。我们不喜欢信任随机数生成器（有太多的故障，许多漏洞与坏RGN有关），因此我们通常使用rfc6979，并根据我们的秘密和要签名的消息计算确定的K值。

使用私钥PK，我们可以为消息M生成一个签名，其中包含两个数字：R（随机点的x坐标R=k×g）和S=（Z+R⋅PK）/k。然后，使用我们的公钥p=PK×g，任何人都可以通过检查点的x坐标（Z/S）×g+（R/S）×p等于R来验证我们的签名。

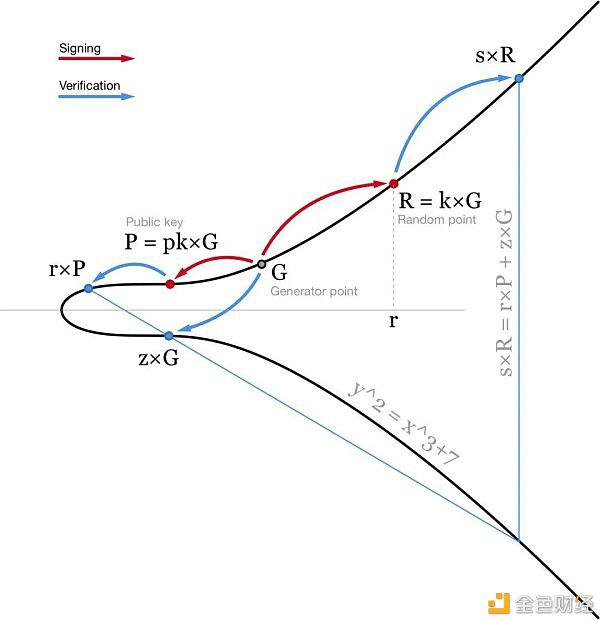
签名验证包括求逆（1/s）和两点乘法，需要大量的计算。在比特币中，每个节点必须验证所有交易。这意味着，当你播出一个交易，成千上万的电脑将不得不验证你的签名。而且简化验证过程将非常有益，即使签名过程将更加困难。

其次，每个节点必须分别验证每个签名。如果是N取M多签名事务节点，则可能需要多次验证同一签名。例如，一个具有7-of-11多重签名输入的事务将包含7个签名，并且网络中的每个节点需要7-11签名验证。再说一次，这样的交易占用了很多空间，你必须为此付出很多代价。

施诺尔签名

Schnorr签名算法是由德国数学家和密码学家Claus Schnorr提出的。他在1990年申请了一项专利，即美国专利4995082，2008年2月到期。目前，该算法可以自由使用。

Schnorr签名生成略有不同，我们使用一个点R和一个标量s来代替两个标量（R，s）。与ECDSA相似，R是椭圆曲线上的一个随机点（R=k×g）。签名计算的第二部分略有不同：

S=K+散列（P，R，m）⋅PK。这里PK是您的私钥，P=PK×G是您的公钥，M是消息。然后可以通过检查s×g=R+hash（P，R，m）×P来验证签名。

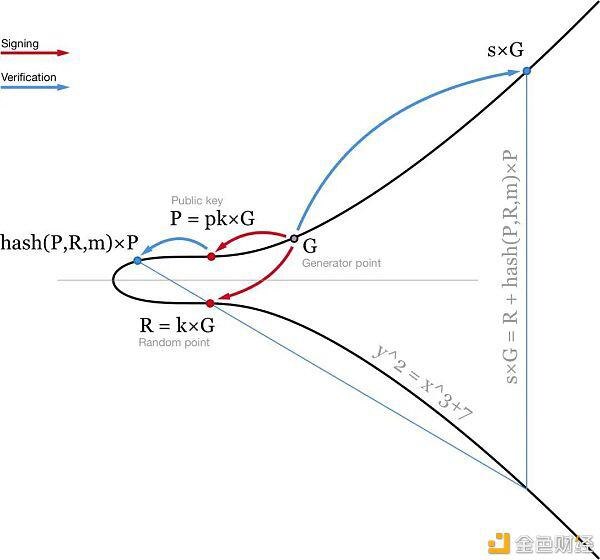
这个方程是线性的，所以方程之间可以加减，而且仍然有效，这给我们带来了Schnorr签名的一些好处。

Schnorr签名的批量验证

为了验证比特币区块链中的块，我们需要确保块中的所有签名都是有效的。

对于ECDSA签名算法，每个签名必须分别进行验证。也就是说，如果块中有1000个签名，我们需要计算1000个求逆运算和2000个点乘运算，总共需要3000个左右繁重的计算任务。

通过使用Schnorr签名，我们可以添加所有的签名验证方程，以节省一些算力。对于具有1000个签名的块，我们需要验证：

（s1+s2+…+s1000）×G=（R1+…+R1000）+（散列（P1，R1，m1）×P1+散列（P2，R2，m2）×P2+…+散列（P1000，R1000，m1000）×P1000）

这里我们有一堆加法（几乎没有算力）和1001点乘法。我们需要为每个签名计算大约一次繁重的计算。

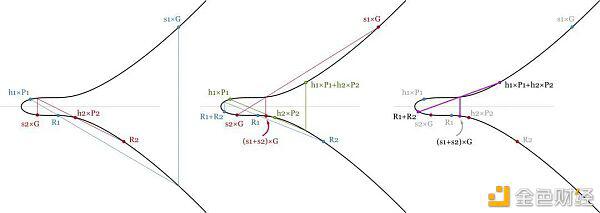
Schnorr签名的密钥聚合

我们希望保持比特币的安全，因此我们可能希望使用至少两个不同的私钥来控制我们的比特币。例如，一个在笔记本电脑或移动电话中，另一个在硬件钱包/冷钱包中。所以当其中一个受到威胁时，我们仍然可以控制我们的比特币。

目前，它是通过2/2多重签名脚本实现的，该脚本要求在事务中包含两个单独的签名。使用Schnorr签名，我们可以使用一对私钥（PK1，PK2），生成一个与共享公钥p=P1+P2=PK1×G+PK2×G相对应的共享签名。要生成这个签名，我们需要在每个设备上选择一个随机数（K1，K2），生成一个随机点RI=ki×G，将它们相加，计算一个公共散列（p，R1+R2，m），然后从每个设备获得S1和S2（Si=ki+hash（P，R，m）⋅PKI）。然后我们可以添加这些签名，并使用一对（R，s）=（R1+R2，S1+S2）作为我们对共享公钥P的签名。没有人可以说它是否是聚合签名。它看起来就像一个普通的施诺尔签名。

这一建设存在三个问题。首先，从用户界面的角度来看，要进行事务处理，需要进行几轮通信，计算出公共R，然后-签名。使用两个私钥，我们只需访问冷钱包一次即可完成：我们在网上钱包上准备一笔未预订的交易，选择K1，并将R1=K1×g与未预订的交易一起记录。然后我们将数据发送到冷钱包并签名。因为我们已经有了R1，我们可以一次签一笔交易。从冷钱包，我们得到R2和S2和转移回网上钱包。在线钱包使用先前选择的（K1，R1）对交易进行签名，合并签名并广播签名交易。这与我们现在所拥有的非常相似，但是一旦我们添加了第三个私钥，一切就会变得更加复杂。例如，您有一笔财富，由10个私钥控制，这些私钥存储在世界各地不同的安全位置，然后您需要进行交易。目前，您只需要浏览所有这些位置一次，但是如果您使用的是密钥聚合，则需要执行两次以组装所有RI，然后签名。在这种情况下，**保留一个单独的签名而不进行聚合，然后我们需要三轮通信：

选择一个随机数Ki和对应的RI=Ki×g，然后只告诉大家它的hash Ti=hash（RI），这样大家就可以确定，你在学习其他随机数后不会改变主意；

把所有的数字放在一起，计算公共R；

签名；

第二个问题是已知的恶意密钥攻击。本文和本文都对它们进行了很好的描述，所以我不想详细讨论它们。这个想法是，如果你的一个设备被黑客攻击（比如说，你的在线钱包），并假装它的公钥是（P1-P2），那么它可以使用它的私钥PK1来控制共享资金。一个简单的解决方案是在设置设备时使用相应的私钥对公钥进行签名。

还有第三个重要问题。确定性K不能用于签名。有一种简单的攻击方法，如果你使用确定性K，它允许黑客获取我们的私钥。攻击看起来是这样的：有人入侵了我们的笔记本电脑，完全控制了两个私钥中的一个（如PK1）。我们可能会感到安全，因为我们的比特币需要来自PK1和PK2的聚合签名。所以我们试着像往常一样交易，准备一个未签名的交易和R1值，把它们转移到我们的硬件钱包里，然后在那里签名。然后返回（R2，S2），我们的在线钱包出了问题，无法签名和广播。我们又试了一次，但这次被电脑入侵，使用了另一个随机值R1#39；。我们再次与我们的硬件钱包签署同样的协议，并将价值（R2，S2）带回我们被黑客攻击的电脑。然后发生了不好的事情，我们的比特币丢了。

在这次攻击中，黑客为同一个事务获取一对有效的签名：（R1、S1、S1、R2、S2）和（R13535353539；，S1\35散列（P，R1+R2，m）-散列（P，R1\39；），m） ）。我发现这是密钥聚合最不方便的特性：我们需要到处使用好的随机数生成器来使用密钥聚合。

彩虹签名

彩虹是一个多变量签名方案。它的层次结构是基于不平衡油流（uov）签名方案。彩虹层的额外结构使得方案面临更多的密码分析技术，但提高了方案的效率。彩虹提供了快速签名和验证以及非常短的签名，但具有非常大的公钥。

Rainbow增加了入围签名方案的多样性，但是由于密钥的大容量，Rainbow不适合作为一种通用的签名算法来代替fips186-4中现有的算法。特别是，大公钥使得证书链非常大。但是，有些应用程序不需要频繁发送密钥。对于这样的应用，彩虹提供了小而快速的签名。