如何利用套利建立最短路径

；

谁不喜欢赚钱？

如果你能把赚钱的问题变成寻找最短路径的问题呢？我们至少可以通过一种特定的方式做到这一点：利用套利机会。

什么是套利？

套利是指商品在不同市场或以不同形式进行交易，从价差中获利的行为。有关人员怎么办？他们被称为套利者，这真是一个花哨的头衔。

让我们从一个例子开始。假设保罗、彼得和鲍勃住在一个村子里，用胡萝卜、土豆和莴苣交换食物。鲍勃用土豆换胡萝卜，彼得用莴苣换土豆，保罗用莴苣换胡萝卜。

此外，鲍勃用两个土豆换了一个胡萝卜，彼得用一个莴苣换了两个土豆，保罗用两个胡萝卜换了一个莴苣。如果我们把每个人都当作自己产品的市场，汇率会是多少？

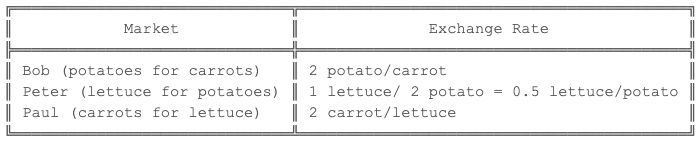
你认为有机会吗？

作为一个有进取心的人，你可以尝试使用它。从5个胡萝卜开始，你接近保罗，用5个胡萝卜换10个土豆，以他愿意的价格。

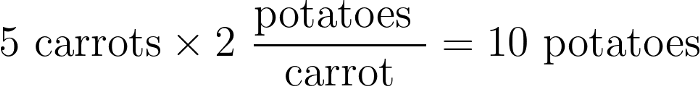
接下来，你带着你的土豆去见彼得，他会用五个莴苣换土豆。然后你拿着5个莴苣接近保罗，他用10个胡萝卜换你的莴苣。

经过几次明智的交易，你的胡萝卜财富翻了一番。利用套利机会，你可以把5个胡萝卜变成10个。

后来，村民们可能会开发出更复杂的市场，鲍勃、彼得和保罗并不是唯一的投资者。相反，村里可以发展一个胡萝卜/生菜市场，一个生菜/土豆市场，一个土豆/胡萝卜市场，每笔交易的汇率会根据人们的交易意愿而浮动。

但套利原则没有改变，在没有胡萝卜、生菜或土豆供愿意以这种汇率交易的交易员使用之前，这些机会是可以利用的。利用套利机会，直到市场达到均衡。

现代套利

当你想到现代市场时，你可能不会想到交易胡萝卜、土豆和莴苣。如果你投资外汇交易，你更有可能考虑交易美元、英镑和日元。在这种情况下，我们将面临美元/英镑市场、英镑/日元市场和日元/美元市场。每个市场都有许多投资者。从现在开始，让我们用这些商品币作为交易的一个例子，但是请记住，这些原则适用于所有可以交易的对象。

在给定时间，汇率如下：

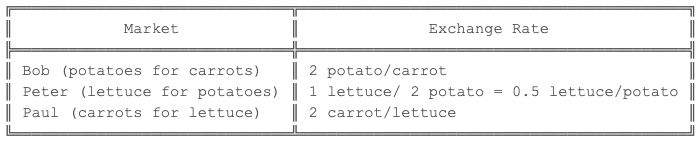
如果你从鲍勃、彼得和保罗的胡萝卜、生菜和土豆交易中学到了什么，你会在这里找到机会。

如果你把一美元换成一英镑，你**会得到0.8英镑。如果你把它换成日元，你会得到80日元。你把日元带到日元兑美元兑换处，在那里你可以兑换美元，但是现在你有1.04美元了！

但在另一个套利者击败你之前，你必须迅速行动。在流动性耗尽和利率平衡之前，这些机会只是暂时的。

你们中的一些人可能会注意到，在我们的示例中，我们没有考虑交易成本。当然，为了计算盈利套利机会是否真的存在，你必须考虑这些因素。

快速反应

我希望你有一些直觉来理解为什么快速行动是必要的。汇率波动很快，可供选择的“东西”有限。

尽管我们在这里使用的是相对简单的例子，但套利机会可以跨越许多交易，变得极其复杂。我们的示例使用3个事务，但是如果需要10个事务怎么办？在一个由20种币组成的网络中，每对币都有一个市场。你能很快找到机会吗？

使用计算机是一个明显的答案，但我们需要一个有效的算法，这样别人就不会打败我们。

要做到这一点，我们可以利用数学和计算机科学的一些聪明的见解。

市场地图

图表是一种非常重要的结构，在许多应用中得到了广泛的应用。许多社会和自然结构都可以用图形来表示。原来市场就是其中之一。

在我们的示例中，让我们将每个装运币视为一个节点。从一个节点移动到另一个节点相当于将一种商品币交换为另一种商品。

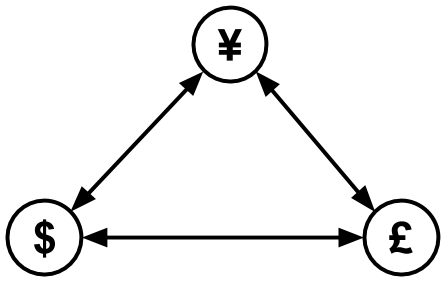
所以沿着节点之间的边缘移动，我们可以通过汇率来转换币的商品数量。

这意味着从美元节点移动到英镑节点相当于乘以0.8英镑/美元。让我们把汇率分配给每一方的权重。

注意，每个方向的汇率都是相互倒数。这意味着，如果英镑对美元的汇率为0.8英镑/美元，则相反的汇率为1/（0.8英镑/美元）=1.25美元/美元。对我们来说，结果是我们需要谨慎对待每个市场的交易，因为不同的定向边具有不同的权重。

之所以双向汇率只近似于倒数，是因为币交易商品的价差很小，称为买卖价差。例如，如果在某一特定时刻，你可以以每美元0.8磅的价格（有人将向你出售的当前价格）购买英镑，但你可以以每美元0.82磅的价格（或每磅1.22美元，有人将向你购买的当前价格）出售每磅美元，那么您的图形模将如下所示（为了简单起见，不包括其他汇率）：-

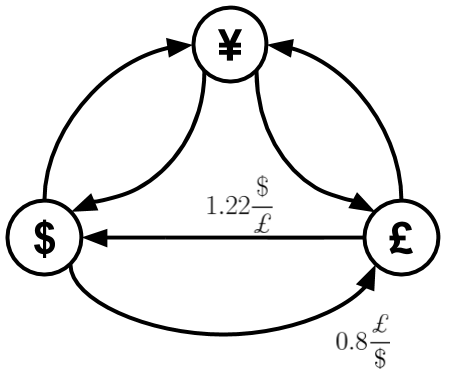
通过沿图中的边移动，可以对一系列事务进行建模，并通过将边权重乘以边权重来计算事务的结果。

看到机会

既然我们有了一个可行的模，我们在对应套利机会的图表中寻找什么？

为了确定一系列交易是否盈利，我们需要一个一致的盈利指标。换句话说，如果我们以美元开始一系列交易，那么我们也需要以美元结束。通过比较最终金额和初始金额，我们知道它是否有利可图。

在我们的图中，这意味着我们的一系列事务必须在它们开始的同一节点结束。在本例中，我们从dollar节点开始，以dollar节点结束。在图表术语中，我们称之为周期。所以我们知道我们在寻找某种循环，但什么样的循环能让它盈利呢？

注意，如果我们沿着周期的边缘相乘，我们将转换为有效汇率的单位。
；

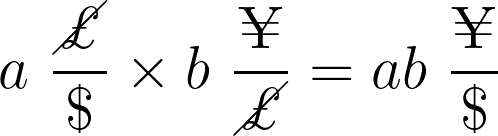
但是，当我们返回到起始节点时，数量变为无单位。它是从汇率转换成回报率的！在我们的图表上遍历一个周期并计算汇率积等于在完成一系列交易后计算回报率。

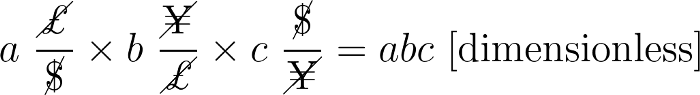
如果市场完全有效，我们的收益率ABC将是1，因为汇率已经相等了。如果权重的乘积大于1，例如1.02，那么套利机会将为我们带来2%的回报。

因此，对于任意数量的交易，套利机会对应以下不等式：

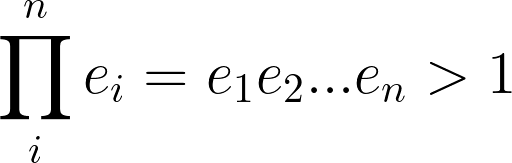
式中，ei对应于第I个汇率。对于每个事务I，除以N个事务。

所以我们需要的是一个算法，可以在市场图中找到一个循环，其中边权重的乘积大于1。你也许可以发明一种算法来解决这个问题，但是在计算机科学中，就像在日常生活中一样，把一个问题简化成你已经知道如何解决的问题是很有用的。

贝尔曼-福特算法

寻找最短路径是计算机科学中一个常见的基本问题，它可以应用于许多不同的场景。通过绘制图形与地图的对应关系，一个明显的方法就是在地图上寻找最短路径。然而，通过一些技术，许多其他类的问题也可以转化为最短路径问题。我想证明的是，寻找套利机会的问题就是其中之一。

首先，让我们确定什么是最短路径问题。给定图中的两个节点s和T，最短路径就是使边权和最短的路径。换句话说，我们沿着从s到t的路径移动，沿着路径添加边权重。总的来说，最短路径就是最短路径，也是代价最小的路径。

接下来，将有助于理解不同类别的最短路径问题。在明显的例子中，例如地图上的最短路线，边权重必须为正。除非有时间机器，否则沿路开车会减少你的旅行时间。在只有正边权的图中，Dijkstra的**算法计算到图中所有节点的最短路径。

然而，没有理由说图形不能有负的边权重。在这种情况下，沿边移动可以减少路径的总开销。但是，如果循环的权重为负，则可以连续遍历循环—每次都减少路径的总体成本，而最短路径的成本接近-infin；。在这种情况下，我们的最短路径算法有一个确定负权重周期的机制是非常有用的。否则，最短路径总是陷入负权重循环。

bellman-Ford算法就是这个算法。Dijkstra最短路径算法的一个更通用的版本，它可以处理负权重。为此，它检测负权重时段mdash；mdash；图中的时段，并将权重相加以产生负值。

然而，当我们需要一个算法来检测边积大于1的环时，如何找到边积小于0的环呢？

登录救援

下一点是乘积可以通过使用对数函数转换为和，这得益于以下等式：

；

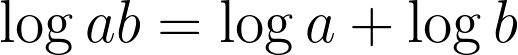
因此，我们可以把乘积大于1的周期问题转化为和大于0的周期问题！我们把每一个汇率的对数作为每一方的权重。

让我们通过记录不等式两边的对数来证明这一点。首先，取左边的对数，将乘积的计算转换为计算的和

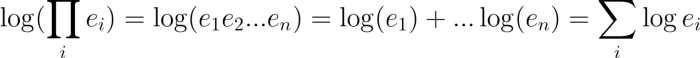
右边的对数只是将1转换为0：

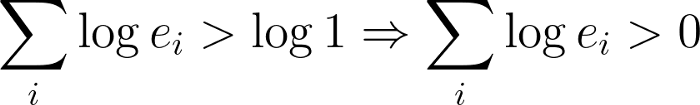
我们很接近，但不太接近。**一步是将我们的问题简化为一个我们可以用这个已知算法来解决的问题，即将每个边的权重乘以-1。这就把寻找正周期和负周期的问题转化为寻找负加权周期的问题

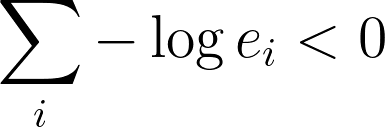
我们知道贝尔曼福特算法可以做到！将套利问题转化为寻找最短路径（即无限最短路径）的问题，按照指定的方法构造图并在图上执行bellman-Ford算法，将有助于快速有效地找到套利机会。

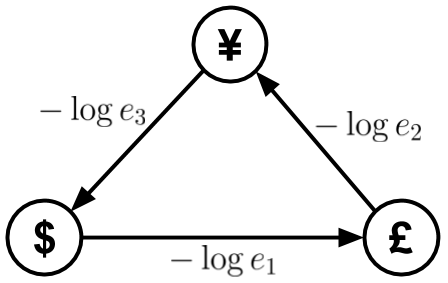
现在看来，负加权周期（每次穿过它都会降低路径成本）和套利机会（每次都能盈利）之间应该有一个对应关系。关键是通过对边权值施加log，将求大于1的积的问题转化为求小于0的和的问题。

证明一下

让我们在汇率上运行这个算法，看看它是否正确识别套利机会。通过对数汇率换算，得到如下结果：

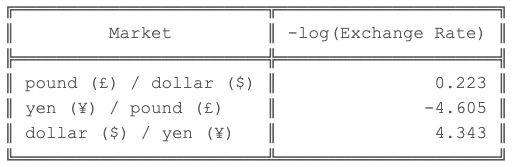
总而言之，我们的平等是建立起来的，我们发现了一个负的重量循环！

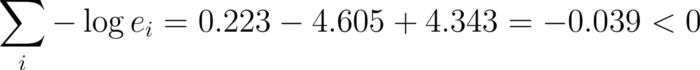
我们可以撤消对数运算来恢复产品并计算收益：

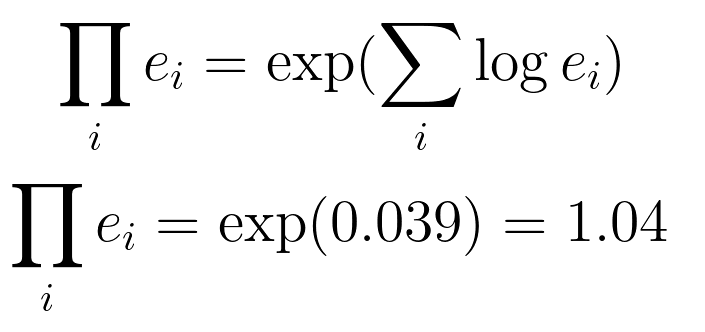
这是我们之前计算的4%的回报率。

在现实世界里

由于套利机会对应于负权重周期，我们似乎可以通过这个周期永远赚无限的钱。当然，事实并非如此。

任何套利机会的可用流动性（价格发生重大变化前的可用金额）都是有限的，并且很快就被算法投资者所利用，从而使计算和物理定律的界限相互对立。

说到这里，我希望你能用图论和**的最短路径算法来解决财务问题（并赚钱），这和我一直以来都很有趣。