信道网络中再平衡算法的加速

在对支付网络中的路由问题进行了全面研究之后，nervos的小伙伴Shor对信道网络中的再平衡算法进行了详细的研究。

本文将介绍信道网络（CN）中的再平衡问题。首先，我们将介绍问题的定义和现有的算法。然后介绍了必要的图论基础和建模方法。**，提出了一种算法加速的思想。（本文假设读者对频道网络有共同的了解。）

我们把支付网络看作一个无向图。图中的每个节点代表一个PID，每条边代表一个支付通道。每条边在图的每一端都有一个余量。注：我们默认每个（双向）支付渠道的总库存量是守恒的。也就是说，在由a和B组成的渠道中，如果a的余额为50，B的余额为80，B向a支付10元后，a的余额为60，B的余额为70。

有时，由于网络拓扑和其他原因，支付渠道的一个方向总是比另一个方向“更受欢迎”。在这种情况下，每个频道的有限总库存被“STARKING”到一侧，或者“流行方向”的流量耗尽。因此，支付网络将频频爆出渠道流量，不得不“上线”重新开通新渠道。再平衡试图通过以下方式缓解这一问题。

例如，在下图中，我们考虑一个由四个边组成的循环，其在主流方向上的10个边距已经用尽。

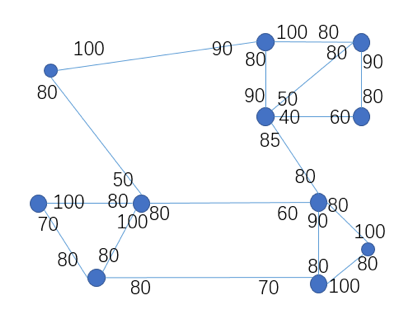
其中每个箭头a660202表示连接a和B的无方向通道，其中a的股票为a，B的股票为B。值得注意的是，箭头方向代表主流方向，因此我们绘制了一个有向图，但**的基于RBR的支付渠道是双向的。通过全球***的协调，Revieve完成了重新平衡的努力（本文中我们将不考虑如何实现该***）。例如，我们可以协调5个单元从B到a，5个单元从a到C，5个单元从C到D，5个单元从D到B，这样整体结构如下图所示。本质上，它是寻找一个“环路”，在这个环路中，所有的通道都以与主流相反的方向返回，以抵消一些流量。

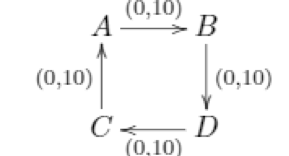
当我们谈论再平衡时，我们试图解决哪些问题？

**强连通分量完成了对任意OKEX交易所有向图所有节点的划分。

有一种高效的o（n）算法可用于求任意有向图的所有**强连通分量（具体算法在本文中不作讨论）。

我们把每个**强连通分量看作一个整体，将所有具有边的存取关系分量连接起来，并对其进行点的约简，得到一个有向无环图。

接下来，我们介绍具体的算法。

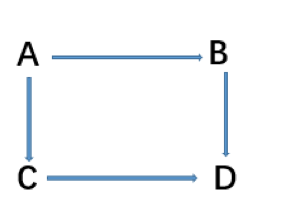
首先，我们对原有的支付网络图做了一个简单的修改，将每个双向的渠道从库存较多的渠道转换为库存较少的渠道的一条有向边，而这一方的能力是两端差额的一半。例如，在下图中，我们将上图转换为下图。

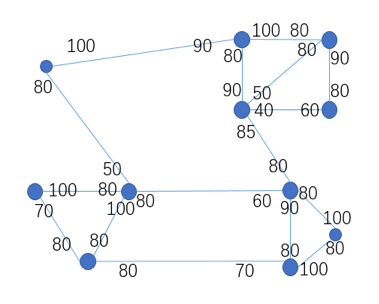
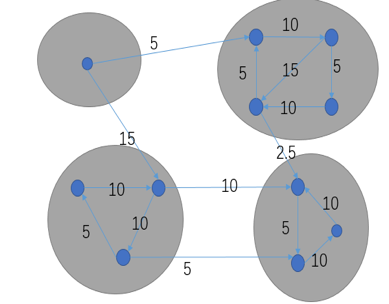
因此，我们将寻找环的问题转化为在有向图中寻找环的问题。有向图的每一条边代表一个“势能”，它需要回流，以便使原始图的相应通道更加平衡。每个回路可被视为回流方案。在对强连通分量进行约简后，我们只需要通过现有的线性规划来求解每个**强连通分量的再平衡问题。

其解是明确的：我们只需求解有向图的所有**强连通分量，在每个**强连通分量中，通过传统的线性规划就可以得到一个**的调度方案。因为我们不认为每一个回路都会跨越两个不同的**强连通分量，所以我们认为该方法是全局**调度方案。

这里有一个小问题：这真的是一个等价的转换吗？不是（虽然乍一看）不是。**全局调度方案中的一个回路有可能跨越两个**强连通分量，因为“多数人需要忍受几个人”（“少数人需要更不平衡以使更多的边更平衡”）可以得到更好的解。然而，笔者认为这种偏差是值得的。而且，到了现实中，也许这几个人不会接受这样的日程安排。

细心的读者应该发现这篇文章中没有解释清楚的两个问题

1优化了多少？

将来连接的组件越多，效果就越强。本质上，问题在于未来大规模支付网络的拓扑结构会是什么样子。可以预期，当绝大多数节点的度仅为4度时，**强连通分量的期望数约为以低于线性速度增长的网络节点数。

2（伪）等价变换的代价是多少？

事实上，这两个问题本质上是在问：未来大规模信道网络的拓扑结构是什么？

在我看来，不仅作者不能回答这个问题，而且没有人能够准确地回答它。这在上一篇文章“支付网络路由综合研究”中已经有了解释。