最新范式研究：uniswap的金融炼金术

研究人员认为，尽管Uniswap流动性提供商（LP）在每一笔套利交易中都会遭受损失，但在某些情况下，由于波动性收益，他们仍然可以比单纯持有货币表现得更好。在这种情况下，收费设置应尽可能接近于零，而不是零，以便尽可能地重新平衡。

本文作者是投资公司paradigment的大卫•怀特、马丁•塔西、查理•诺伊斯和丹•罗宾逊，他们是Uniswap的种子轮投资者。

在无情的套利下，Uniswap LP变得富有起来。

1、 问题

10月14日，查理·诺伊斯在推特上发布了他和丹·罗宾逊一直在争论的一个问题：

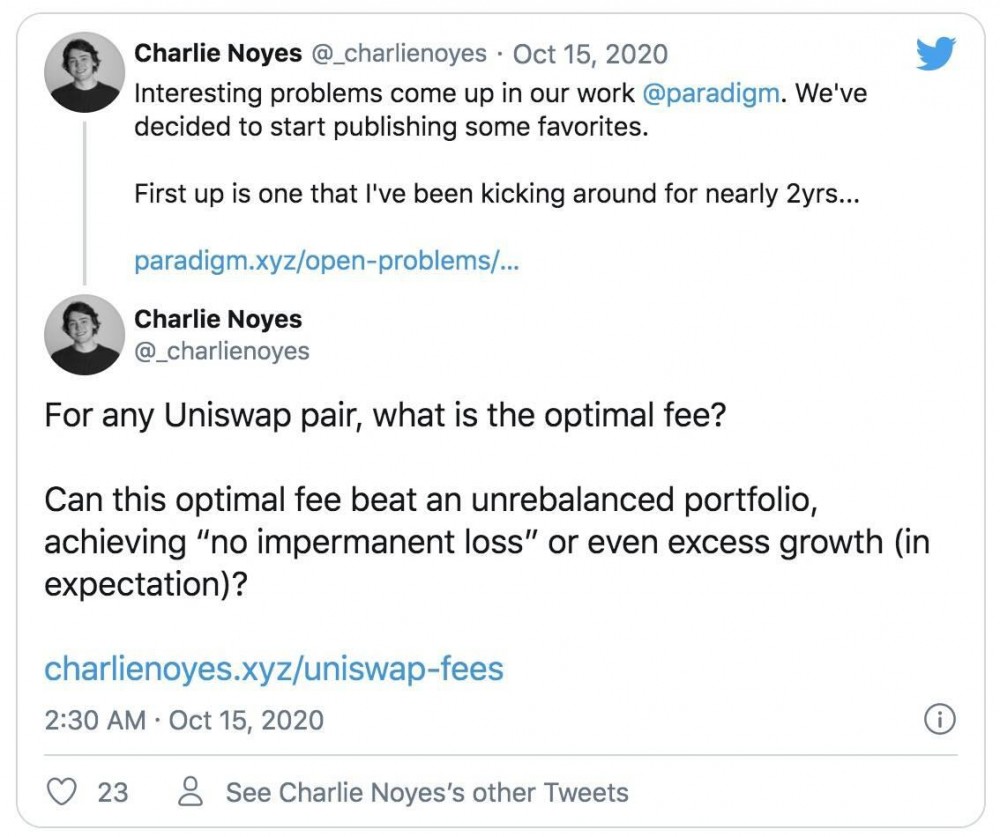
“任何Uniswap资产对的**费用是多少？这种**成本能否战胜不平衡的投资组合，消除波动性损失甚至超额增长

11背景

自动做市商（AMM）是一种去中心化的交易所，允许客户在诸如USDC和ETH等链上资产之间进行交易。Uniswap是以太坊上***的AMM。与大多数资产管理系统一样，Uniswap通过持有两类资产的储备来促进特定资产对之间的交易。它根据外汇储备的规模来决定它们之间的交易价格，从而使价格与更大的市场保持一致。

任何愿意加入某对资产池的人，我们称之为流动性提供者，简称LP。这些人将同时向两个储备资产提供资产。他们必须承担部分交易风险，以换取部分费用回报。

12设置问题

该池提供稳定币和随机价格变化的风险资产之间的流动性。我们还做了一个特别残酷的假设，即所有进入资金池的交易都是知情的（只有当AMM价格与正常交易价格之间存在抵消时才会发生套利）。

换句话说，每次交易后，整个资金池都会遭受损失。

13传统思维

乍一看，在这种情况下，成为Uniswap LP似乎是一个代价高昂的错误。

因为做市商要求买入价低于卖出价，当资产价格不动时，做市商直接获利，买卖量基本平衡。这些交易通常被称为“不知情”交易，因为它们与短期价格变动无关。

另一方面，做市商在价格下跌前买入资产，或在价格上涨前卖出资产，就会亏损。因此，做市商最担心的交易对手之一就是套利。他们只会在价格变化时进行交易，而把做市商抛在后面。套利者进行的每一笔交易对他来说都是净利润，但对做市商来说则是纯粹的亏损。

由于在我们的Uniswap问题设置中没有未告知的交易（事实上，我们假设每个交易都是套利交易），很明显，LP将遭受非常大的损失。

1挑战4

但是，丹和查理不认为这就是故事的结局。

他们怀疑，对于一些潜在的价格动态，成为Uniswap LP仍然有意义。

然后我和史瑞一起为史蒂夫和马蒂解决了这个问题，然后他们在金融领域提出了解决问题的办法。

在接下来的几周里，我们四个人花了一些时间来记录结果，寻找错误，建立我们的直觉，这些讨论是本文的基础。

2、 解决方案

如果一项资产相对于其平均回报率的波动性足够高，那么随着时间的推移，Uniswap上的LP将比Hodler表现更好，即使所有交易都是套利交易。

这是由于一种被称为“波动性收获”的现象：在某些条件下，通过周期性地重新平衡两种资产，它们的表现很可能超过任何静态投资组合。在这种情况下，“再平衡”是指将持有的每项资产的总投资组合价值的一部分返还给固定配置，例如50/50。

因此，当LP被套利时，他们基本上会向市场支付一笔费用，以重新平衡其投资组合。在这种特殊的数学环境中，当这种再平衡是有益的，你应该尽可能多地去做。这意味着流动性提供者应该将他们的收费定得尽可能低，而不是零。

这对Uniswap来说是个好消息，因为这意味着即使套利交易占主导地位，它仍然可以享受低费用，这使得Uniswap具有竞争力，因为连锁订单增加，并开始提供更小的价差。

换言之，值得重申的是，这些结果适用于非常特殊的数学设置，所涉及的假设与Black-Scholes期权定价模非常相似。为了数学上的方便，我们还假设了与Uniswap生产中使用的不同的成本结构。

21控制标准

我们通过比较它们的增量财富增长率来评估不同的策略，这些增长率衡量它们在长期内复合（或损失）价值的速度。

这个数字很重要，因为随着时间的推移，优化它的策略比几乎不确定的策略表现得更好。

我们把所有的策略比作一个“不平衡的投资组合”，其中一半的价值是稳定币，另一半是风险资产，这在那之后永远不会改变。这也是衡量AMM中所谓“无常之失”的社区标准。

无论发生什么，不平衡的投资组合总是持有相同数量的稳定币，这意味着在最坏的情况下，当风险资产失去其全部价值时，不平衡的投资组合几乎全部由稳定币组成，因此长期来看增长率将为零。

另一方面，如果风险资产呈指数增长，很快就会成为主导的非均衡投资组合，因此其增长率与风险资产的增长率相同。

值得注意的是，这两种投资组合可以分享相同的财富增量增长率，但在近距离表现不同。例如，如果风险资产的增长率为零，那么零成本Uniswap的股票价值将始终低于不平衡投资组合的股票价值，但由于两者都不会随着时间的推移而增长或复合损失，其财富增长率将为零。

22波动阻力

50%损失/75%回报过程中的波动阻力（来源）。

要理解这些结果，我们必须首先理解波动阻力的概念。假设我们的风险资产价格每年下降50%或增加75%，两者的概率相等。

在任何一年，如果我们在资产上投资100美元，我们的预期是（50+175）/2=112.5。如果我们简单地买入并持有，我们投资组合的预期价值将同比增长12.5%，这似乎是一笔不错的交易。

不幸的是，在现实世界中，我们的利润不会实现。如果我们购买并持有这样的证券，我们最终将失去一切。

由于时间的推移，财富的累积会导致灾难性的损失。

如果我们在一年内损失50%，然后在下一年增加75%，我们只有87.5%的投资（即50%*175%）。

随着时间的推移，大数定律将保证我们每年的收益为-15%，我们将不可避免地破产。

2等等，怎么了？

如果你受过从期望的角度分析赌博的训练，上一节可能看起来很奇怪，甚至完全不正确。

事实上，一个多星期前，我们对这个问题有了一个完整的、封闭的数学解，在此之前，我直觉上还不知道它意味着什么。

根本原因是：期望是一个理论量，它衡量了如果我们同时在无数平行宇宙中**一个给定的游戏将会发生什么。

但现实并非如此，每一场比赛我们只有一次机会，而我们比赛的效果不是瞬间的，而是随着时间的推移而合成的。

我们可以从另一个角度来看待它，以帮助调和数学。当我们继续重复（-50%/+75%）的游戏，并且每次都将钱进行再投资时，只有极少数路径是正确的，从而产生了天文数字的回报。

随着时间的推移，这些路径在所有可能路径中所占的比例越来越小，我们真正看到其中一条路径实现的机会也将减少到零。

2再平衡的价值

面对波动阻力，即使预期值为正，也应保留部分资金。这样，当事情出了问题，你的损失就会减少，从长远来看，这会增加你的复合财富。

就交易而言，所有这些都导致了一些相当熟悉的概念。当价格上涨时，有时会关闭部分头寸以锁定利润，以防价格再次下跌。当价格下跌时，为了以有利的价格获得预期的未来回报，有时采取下限是有意义的。

在某些情况下，比如这次，**的策略是不断地重新平衡你的投资组合，这样你在每一个头寸上都有固定比例的财富，比如说，一半是稳定币，一半是风险资产。这并不总是**的平衡。一般来说，你希望投资组合中的风险资产越多，其回报相对于它的波动性就越高，但我们将把进一步的探索推迟到未来的工作。

重新平衡长期财富增长的好处是巨大的，可能意味着财富指数增长和破产之间的区别。即使在我们建立的背景下，每一笔再平衡交易都有一个非常负的价格，并且会造成瞬间的损失。

25资源

很可能您对这些解释不满意，希望了解更多。

你可以先回顾一下凯利的公式，这是一个基于这些原则的理论上**的投注策略。@Wpoundstone的财富公式是一本备受推崇且易于阅读的书，内容涉及凯利公式的历史和意义。

在另一篇关于财富增长的文章中，我们强烈推荐彼得的《财富增长》一文。

如果你选择自己做研究，你必须小心。这是一个鲜为人知的领域。在我自己的研究过程中，我发现很多来源是错误的，这使得我的理解倒退了几个小时或几天。

特别是，如果你看到均值回归或对数效用函数的调用，我建议你不要停下来继续前进。这个领域的关键结果不需要假设任何特定的收入分配或效用函数。

2成本Alchemy

在这种情况下，什么时候成为有限合伙人有益？LP是否应尽可能经常地进行再平衡，以**成本促进再平衡？

（收费应尽可能低，而不是零，以便通过越来越小的价格变动触发再平衡。丹罗宾逊称之为“在量子泡泡中捡拾便士”。

然而，当成本完全为零时，再平衡的所有好处都会消失，而且在大多数情况下，LP的情况比只持有不平衡的投资组合更糟糕。

理解这一看似反常的现象有助于揭示问题的其余部分。

Uniswap使用“恒定产品”不变量，这意味着每次交易的储备金余额的乘积必须保持不变而不收费。我们将此表述为

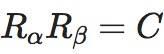
熟悉Uniswap的读者可能更习惯于将其写成X*y=K。

然而，事实证明，为了实现再平衡，这个产品C的数量必须增加，以便为我们提供过剩的财富增长。

为什么C这么重要？我们说；

是我们准备金余额RA和Rb的几何平均值。与算术平均数一样，几何平均数随着储量的增加而增加。然而，与算术平均值不同的是，几何平均值随着储量的不平衡而减小，即使它们的算术平均值保持不变。

C是常数，不收费，所以交易总是导致更大或更平衡的储备。两者从来不会同时存在，因此，财富增长没有动力。

然而，在Uniswap的现实世界中，或者在我们建立的环境中，非零费用保证C将随着每次交易而增加。随着时间的推移，这意味着外汇储备不仅在增长，而且趋于平衡，这将带来上述好处。

为了理解如何计算这一点的精确数学，请参考马丁的第3.1部分和我的证明文件。

3、 数学

说到这里，我们现在可以确切地回答查理在最初的问题陈述中提出的问题。

再次，他们关心的是Uniswap风格的AMM的财富增长率G，其中的百分比是

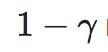
稳定币和波动性资产受带参数的几何布朗运动的影响；

漂移和

波动性）。

31 LP财富增长率

3**成本与超额收益

当且仅在下列情况下，作为有限合伙人持有半稳定币和半风险资产的收益大于仅持有货币的收益：

在这种情况下，有限合伙人应尽可能低而不是零收费，他们将实现财富的逐步增加

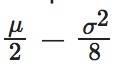
33解释

因为几何布朗运动模拟复合生长，它们也受到波动阻力的影响，其数学表达式为

财富增长率如下：

这意味着

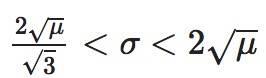
在范围内，**是Uniswap LP而不是

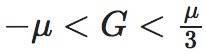
hodl的增长率更为显著。

这让我们对结果有了一个洞察：再平衡使我们能够部分抵消基础资产的波动阻力。如果没有波动阻力，且平均回报率为零或为负，那么再平衡的规模将无济于事。尽管重新平衡的投资组合仍将比仅仅持有资产本身做得更好，但我们**只持有稳定币。

另一方面，如果没有波动阻力，则平均回报率为正

如果波动阻力导致资产损失超过其平均对数回报率的200%，那么在Uniswap上进行再平衡并不能消除足够的阻力，所以你**持有稳定币。

如果抗波动性使得资产损失低于其平均对数回报率的66%，那么在Uniswap上重新平衡是不值得的。你**直接持有资产。

在这个范围内，成为Uniswap LP最终会让你变得富有，事实上，比你所持有的稳定币和波动性资产的任何不平衡投资组合都要富有。这既包括最终将变得一文不值的资产，也包括将呈现抛物线式增长的资产。

34证据

你可以在这里找到完整校样的预印本。其工作原理是建立离散随机游动的动力学模，当步长减小到零时，对其进行动作约束。

你也可以看看我最初的零对数漂移证明，并在这里做一些问题模拟。

3我们应该对这些发现有多信任？

在我个人看来，这是非常可信的。

我们有两种独立的证明方法，它们在字段重叠时产生相同的结果。我们也有一些模拟来验证我们的预测：

模拟和预测财富增长率（来源）。

不过，这是一个非常令人困惑的领域，在过去的几周里，我对它的理解已经改变了很多次。如果您发现错误，请随时与我们联系。

4、 今后的工作

虽然我们希望您同意这些发现在理论上是有趣的（或令人发狂的），但仍有许多工作要做，以确定它们与现实世界的相关性。

例如，我们的许多假设可以修改或扩展：

如何将这些结果转化为多资产案例，或者LP何时可以选择50/50以外的比率（如平衡器）进行再平衡？

当我们不再允许每单位时间进行无限交易时会发生什么？

当我们引入交易成本时会发生什么，交易成本甚至可以改变以反映优惠天然气拍卖的动态？

也存在一些经验问题

我们能估计出今天市场上证券交易的这些参数吗？

有多少活跃的代币可以从我们描述的这种再平衡策略中获益？

我们能否确定因收益波动而在现实生活中实现的Uniswap LP收益的比例？

**，也许最有趣。我们如何利用在这里学到的知识来改进现有的协议，创建一个新的协议，或者开发整个DeFi生态系统？