1了解defi常数函数做市商（cfmm）的曲率权衡（2）

在本系列的第一篇文章中，我们研究了常函数做市商的交易函数曲率对交易者行为的影响。我们还提到了我们的论文“狗尾巴什么时候摇摆？”？“曲率与做市”，这将解释价格稳定与曲率之间的关系。回想一下，非正式地说，cfmm交易函数的曲率描述了cfmm在小交易后报价的**变化。当cfmm为主要市场时，交易对同一资产二级市场的影响取决于两个市场的曲率比。这说明市场间的价格稳定与市场的曲率密切相关。一个自然的问题是：理性流动性提供者（LP）为什么选择将流动性投放到主要市场还是二级市场？或者，他们如何比较这些市场的回报？

在本文中，我们将着重从两个角度回答这些问题

证明了当资产对的均值回归时，LP可以获得**的利润；

在交易者信息条件下，我们度量了有限合伙人面临的逆向选择；

第二种情况下的LP收益，类似于Albert Kyle、Lawrence Glosten以及Paul Milgrom（2020年诺贝尔纪念奖得主）的经典市场微观结构结果。我们将证明，LP收益的这两个方面都与曲率密切相关。这些结果表明，cfmm的形状不仅决定了主要市场的稳定性，而且控制了LP的预期盈亏。

平均回归是**的

对于给定的价格变化，较低曲率的cfmm将给LP带来更多的损失。同时，较低的曲率提供了较低的滑动点，从而吸引了更多的交易者和手续费收入。通过研究波动性损失和成本之间的权衡，LP可以优化其回报。**曲率将取决于市场的行为。在这里，我们可以选择两种模：一种是对独立于市场机制的外部价格过程进行建模，另一种是直接对基础市场微观结构进行建模。

就前者而言，这一过程的相关特征是相关性、波动性和均值回归。对于平均回报资产，“收益率**”曲率通常较低。Cfmm流动性提供者从均值回归中受益，因为准备金恢复到以前的水平，而费用则在两个方向累积。在强平均回报资产的情况下，波动性损失的风险很低，流动性提供者（LP）可以提供较低的曲率来吸引交易员。最**的例子是curve，它的稳定币通常在1美元的价格上徘徊，套利者很快就会纠正偏离这一水平的情况。因此，curve提供了一个超低曲率的cfmm，比Uniswap这样的高曲率池吸引了更多的交易兴趣。只要稳定币继续回归到美元的平均值，曲线LP将比其他具有高曲率cfmm的LP表现更好。在本文中，我们证明了一个简单的结果，即对于平均收益资产，LP的费用取决于曲率

对于正常数Cgt；0。

许多协议具有随时间变化的事务功能。下面，我们看到收益率（左）和名义（右）的边际价格函数。

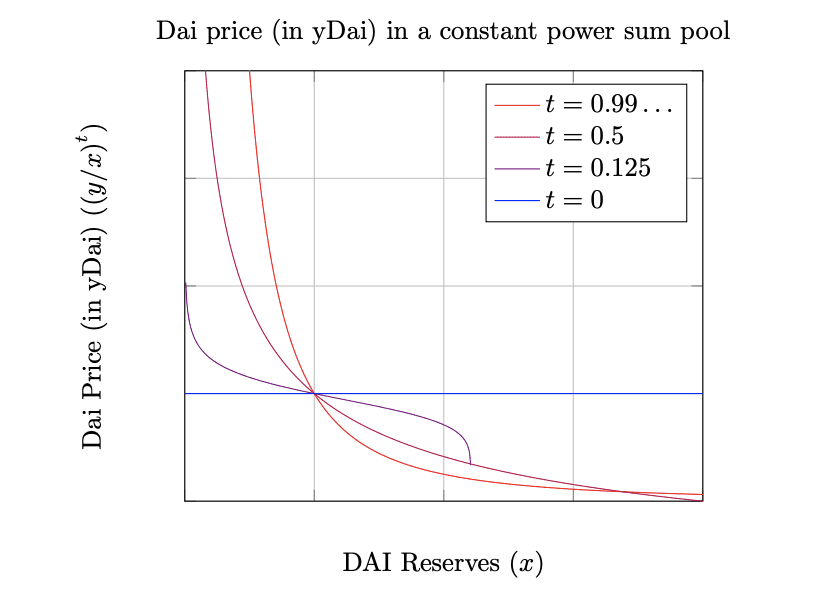
这两个协议的目的是提供固定利率贷款，并有效地利用cfmm的曲率来控制用户的激励。在时间t时，这些系统的用户有效地创建了在t+t到期的固定利率、零息债券。当用户创建债券时，他们将债券投给小于1个债券/1 Dai的债券。用户可以在cfmm市场与Dai进行债券交易，Dai的滑动点反映了提前赎回的成本。这与传统回购市场债券提前赎回类似。当我们接近时间t+t时，cfmm曲率减小，鼓励用户关闭债券（例如，将其作为Dai进行交易）。到期时，cfmm没有曲率，这意味着用户可以按1:1的比例赎回Dai。请注意，当我们接近成熟时，这些cfmm设计鼓励均值回归（例如，达到1:1）。结果表明，在设计该机制时，我们需要调整成本以确保LP是盈利的。

市场微观结构

另一种描述LP收益的方法是考虑LP、套利和知情交易者之间博弈的预期利润。为了构建我们的游戏，我们首先从市场微观结构的传统文献中汲取灵感。在这些文献中，如凯尔的连续拍卖和内幕交易（1985），考虑了做市商与噪音和知情交易者之间的博弈。在这些模中，假设每个参与者都有一个策略来提供他们愿意交易的价格和数量。例如，知情交易者可能知道某项资产的每股收益在上升，并积极买入，直到新的市盈率与原来的市盈率相同。另一方面，做市商有一个策略来产生他们愿意在订单中报价的价格和数量，而噪音交易者则完全随机购买。给定一组市场参与者的策略，我们试图找出是否存在市场均衡，如果存在，是否可以计算。

一般来说，由于计算的复杂性和统计上的原因，在多人博弈中计算精确的均衡是非常困难的。然而，通过研究一个简化的博弈，我们可以获得足够的直觉来设计一个可以估计实际均衡的数值模拟。这是一个只有三个玩家的游戏，凯尔（1985），格洛斯顿和米尔格罗姆（1984）。

在这些博弈中，零利润条件（一种没有套利的弱形式）通常被应用于做市商以达到均衡。零利润条件有效地代表了做市商的盈亏平衡点，是收费和知情交易者信息优势的函数。例如，如果知情交易者的信息优势较弱，他们的交易看起来像“噪音”，而做市商则通过反复越过买卖价差来赚钱，而价格则表现为弱均值回归。另一方面，如果知情交易者是无所不知的，并且总是提前知道未来的价格变化，做市商需要更高的费用和更大的买卖价差来补偿对他们不利的交易。在这种情况下，我们说做市商受到知情交易者逆向选择的影响。事实上，做市商通过减少市场流动性来应对逆向选择的增加。Glosten（1994）指出，当你考虑在多个市场报价的做市商时，指令簿的形状会影响逆向选择导致的流动性变化。在下图中，我们可以看到一个订单有两个不同的形状，一个近似凹，一个Convex。Glosten指出，凹面形状对流动性和低交易速度更有利，而Convex形对于许多小订单和高交易速度更好。

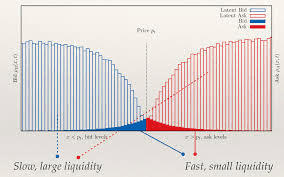
根据伯克利大学Jun aoygi最近的一项研究，通过考虑LP和知情交易者之间的一个简单的单周期博弈，Uniswap的结果与Kyle（1985）相似。他特别指出，噪音交易者只有与Uniswap进行交易，费用才能正确补偿噪音交易者造成的波动，LP才能赚钱。我们在第一篇文章中描述了价格的稳定性。然而，这些结果在很大程度上取决于Uniswap常数积公式的简单函数形式。此外，这些结果并不包括补偿逆向选择所需的精确费用范围。对于其他的cfmm，我们是否可以用更一般的方式将成本与逆向选择联系起来？

因此，我们在套利、知情交易者和有限合伙人之间构建了一个不同的博弈。我们首先将知情交易者定义为在t+1，P（t+1）时刻知道资产价格概率的参与者。

我们把P（T+1）写成P_inf（T），我们可以想象这是一个有见识的交易者在掷硬币。硬币正面落地的概率为0，反面下跌的概率为1小时，如果为正，交易者将正确选择下一个价格。这个有远见的参与者在时间t与cfmm进行交易，并在时间t+1时以概率实现利润。另一方面，如果知情交易者输了，价格将回到时间t的值。示意图如下：

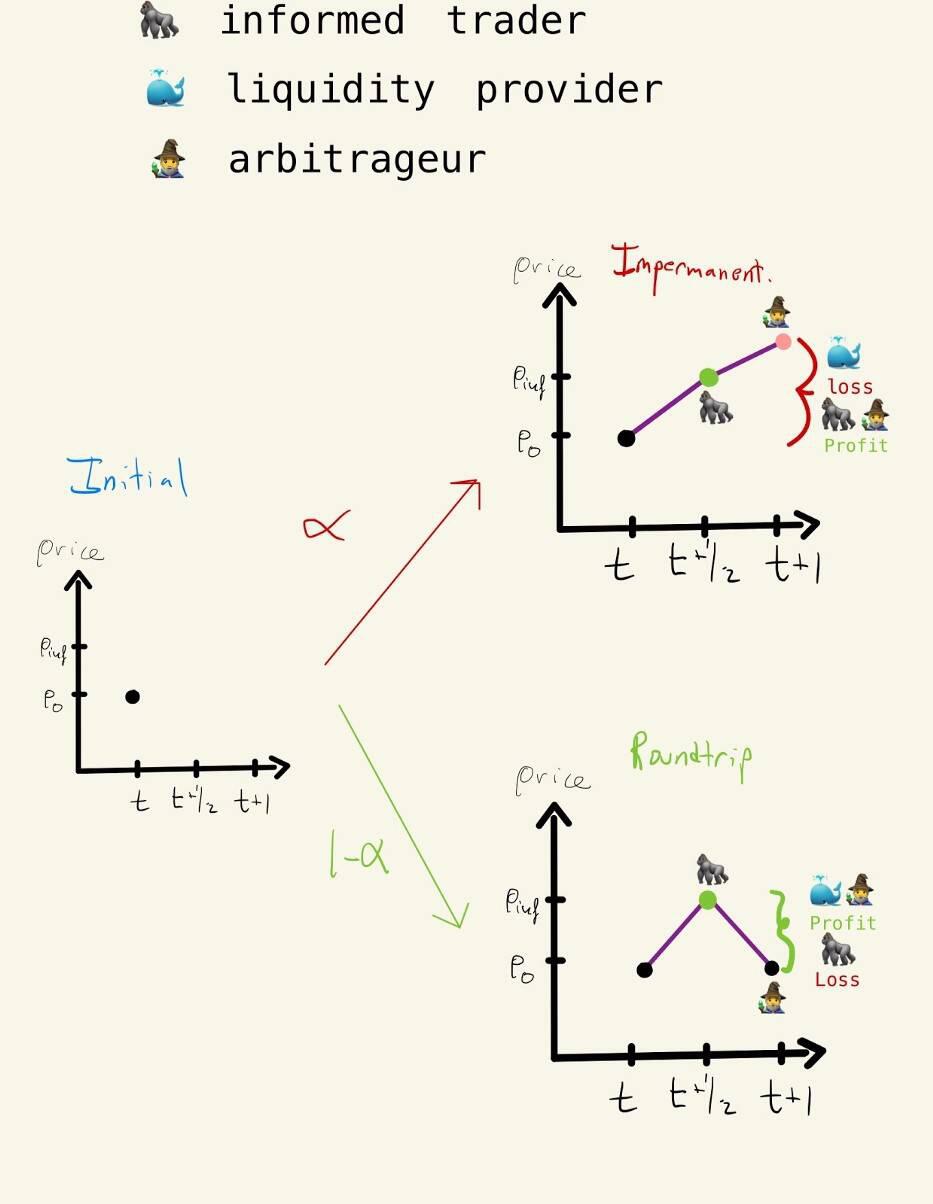
请注意，当知情交易者亏损时，价格会从P（T）变为P_Inf（T），然后再变回P（T）。在这种“往返”交易序列中，流动性提供者获得的利润是成本和cfmm曲率的函数。这意味着我们可以看到流动性提供者的预期利润，PNL（曲率，费用）=?*损失（曲率，费用）+（1-?利润（曲率，费用）。我们用这个期望利润条件来寻找PNL（曲率，费用）gt；0的一个充分条件，并对一些常数Cgt；0找到了这个充分条件

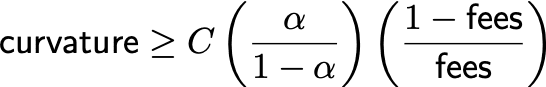
这意味着，如果知情交易者是无所不知的（?=1）或成本为零，则没有曲率可以补偿LP的损失。另一方面，如果知情交易者基本上是一个噪音交易者（??），曲率可以降低，使LP盈利。这一结果表明，与cfmm设计领域的常识不同，人们不仅需要获得**的成本以使LP收益**化，而且还需要调整曲率。我们在现实世界中见过许多这样的例子。例如，dodo和mcdex等保护性做市商已经加入了一个预测机器，以根据主要市场（如Uniswap或CoinBase）的交易调整曲率。在Shell协议中，代价与曲率的关系是直接的。一旦稳定币储备偏离目标权重，则通过动态成本函数将曲率引入交易函数。

在下图中，我们看到了这些协议如何根据其交易活动调整其交易函数曲率的示意图。这通过增加知情交易的反应曲率，有效地减少了逆向选择。目前，大多数曲率调整都是外生的，这需要外部预言器来触发曲线变化。

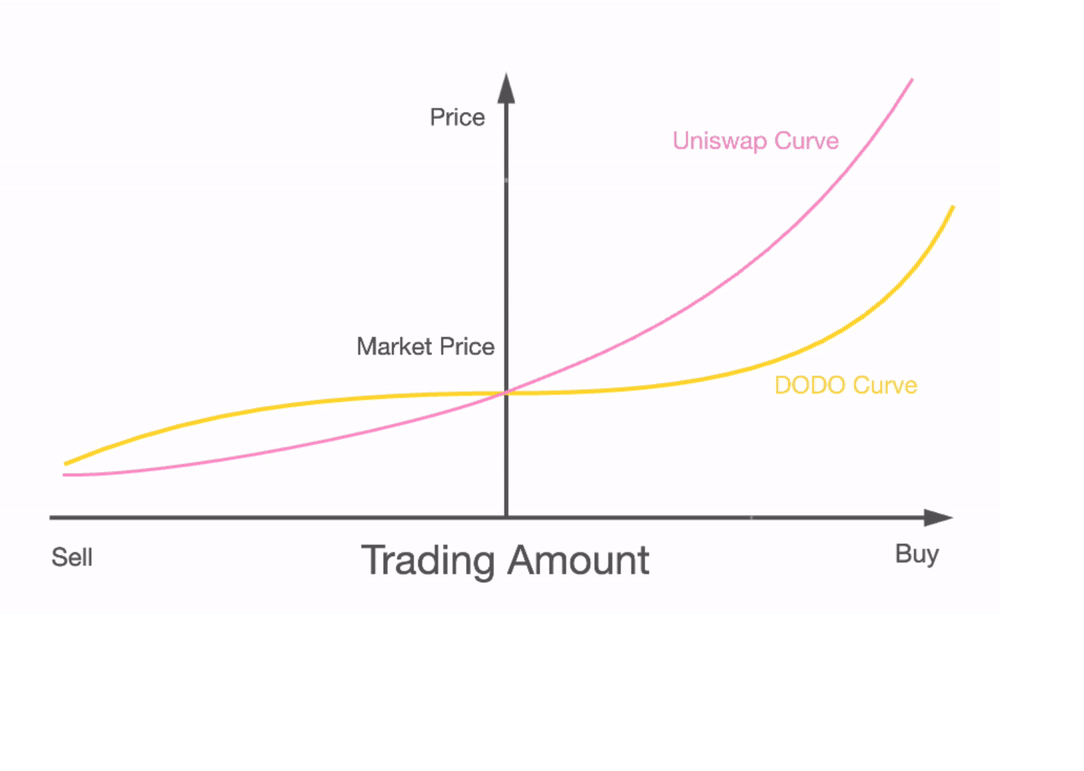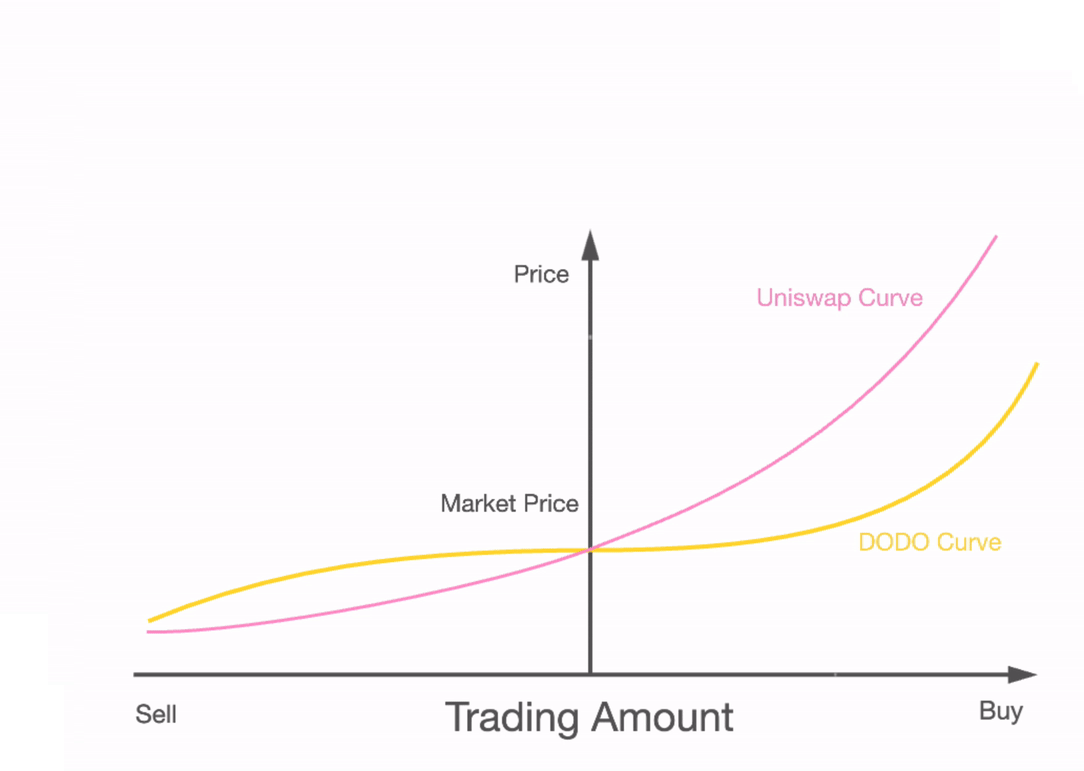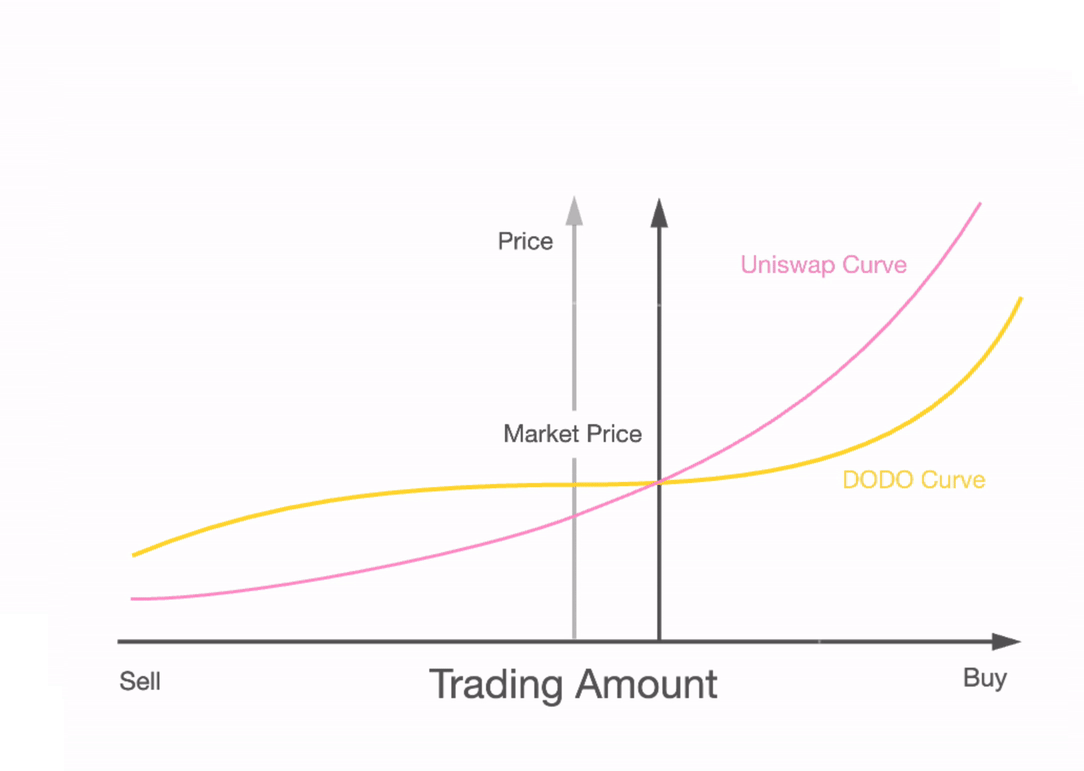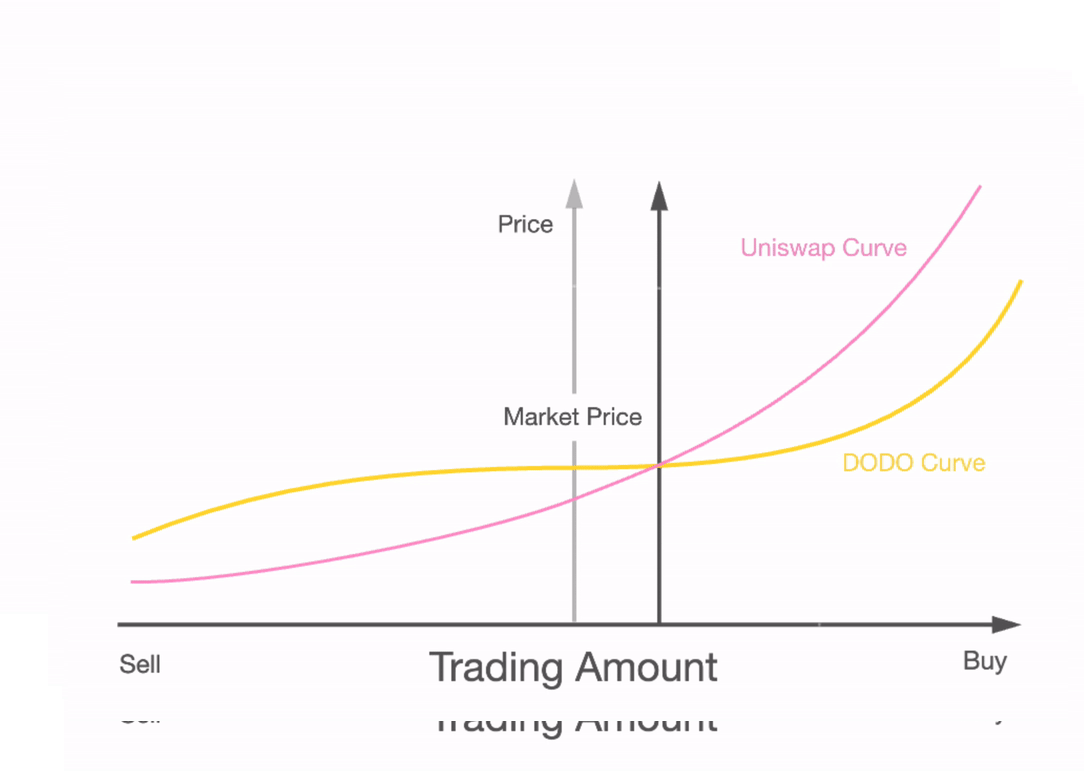
Dodo的协议根据中间价预言机调整曲率

此外，它还告诉我们，活跃和低曲率的cfmm市场（如curve）往往没有多少知情的交易。这符合一种直觉，即用一种稳定币换另一种货币的交易者对未来价格的有用信息较少。

未来cfmm设计

这告诉我们如何设计cfmm？首先，通过设计cfmm的事务函数，利用预言机对曲率进行修正以提高性能。做市商可以有一个动态更新的交易函数来响应交易，以减少LP的波动性损失。更新规则可以是纯内生的（与使用预言机机器的设计不同）和简单的控制机制（类似于DeFi-PID控制器，请参阅我们之前关于这个主题的文章）。同样，cfmm曲率的梯度流（例如，类似于**的Ricci流）可用于自然平坦由于高滑点而交易量较低的区域。不幸的是，这种cfmm不能通过分析来设计。有必要通过模拟具有不同信息量和策略的多个agent与LP交互来设计这种形式的实用cfmm。另外，如果我们看到高频交易中经常出现的复杂性，我们应该预计动态LP策略将成为未来的常态。这些策略对曲率和逆向选择的影响也需要用基于agent的模进行建模。