基于加权卡尔曼滤波的加权卡尔曼滤波

数据融合（DF）或多传感器数据融合（MSDF）是指对来自不同主动或被动传感器的数据或信息进行组合或整合，对数据或信息进行预处理，以生成更精确、更具体、更全面、更统一的数据集、模或决策的过程。随着信息技术的广泛发展，人们提出了更广义的信息融合概念。

李云，孙淑丽，郝刚。基于Gauss-Hermite近似的非线性加权观测融合unscented Kalman滤波器。自动化学报，2019，45（3）：593-603

http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c170534

滤波算法在定位、目标跟踪、导航和故障诊断中起着重要作用。然而，单传感器难以满足高精度和高容错性的要求，多传感器融合估计技术应运而生。近几十年来，线性系统的融合估计理论有了一系列完整的理论基础。目前，常用的信息融合估计方法主要包括两种基本结构：中心化式融合估计和分布式融合估计。中心化式融合估计扩展了所有传感器信息，设计了基于增强观测的融合状态估计。该算法没有信息丢失。当所有传感器无故障时，估计精度具有全局**性。它可以作为其他融合算法精度的衡量标准。它也是多传感器系统中常用的融合方法之一。然而，由于中心化式融合算法计算量大，在传感器数量较多的情况下，中心化式融合算**导致整个系统的实时性较差。特别是当传感器出现故障时，滤波器可能会发散。分布式融合算法是将每个局部状态估计值发送到融合中心，根据一定的融合准则加权得到融合估计值。分布式融合方法鲁棒性好，计算量小，容错性强，估计精度为局部**和全局次优。

加权观测融合算法根据加权最小二乘准则，对中心化式融合系统的增强高维观测值进行压缩，得到降维观测值。基于降维观测值设计的滤波器可以明显减少计算量。对于线性系统，加权观测融合算法在数值上等价于最小方差意义下的中心化式融合算法，具有重要的应用价值。然而，大多数系统都具有非线性特性。例如，大多数定位系统的观测方程是在球坐标系下建立的，而状态估计和分析往往是在笛卡尔坐标系下进行的，这使得观测方程具有一定的非线性特性。

本文的主要创新点和工作如下：首先，采用分段Gauss-Hermite近似方法对系统观测方程进行统一处理，得到了近似的中间函数和系数矩阵。基于中间函数、系数矩阵和加权最小二乘法，提出了一种非线性加权观测融合算法。该融合算法可以压缩增强后的高维观测值，减少后续滤波的计算负担。**，结合UKF滤波算法，提出了一种非线性加权观测融合UKF滤波算法。该算法可以解决非线性多传感器系统的融合估计问题。与中心化式融合UKF（cmf-UKF）算法相比，wmf-UKF具有近似的估计精度，但计算复杂度大大降低。而且，随着传感器数量的增加，wmf-ukf在计算复杂度上的优势将更加明显。

考虑一个有8个传感器的平面跟踪系统。笛卡尔坐标系下的EOS和观测方程如下：

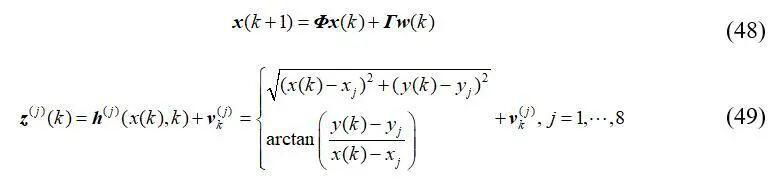
由上述方法得到的融合跟踪曲线如图4-6所示。

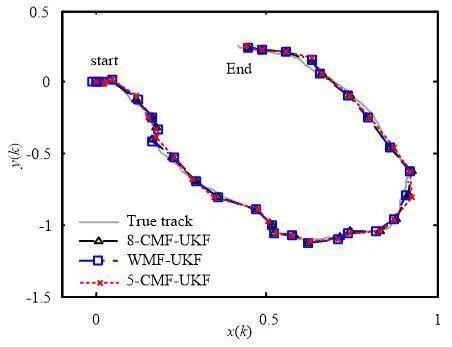
图4 wmf-ukf、8-cmf-ukf和5-cmf-ukf的真实轨迹和估计曲线

图4使用WMF-UKF、8-CMF-UKF和5-CMF-UKF的真实和估计轨迹

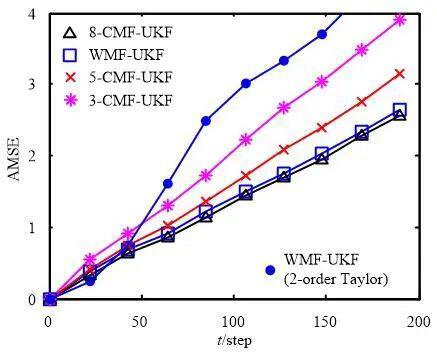
图5位置融合估计的AMSE曲线

图5位置融合估计的AMSE曲线

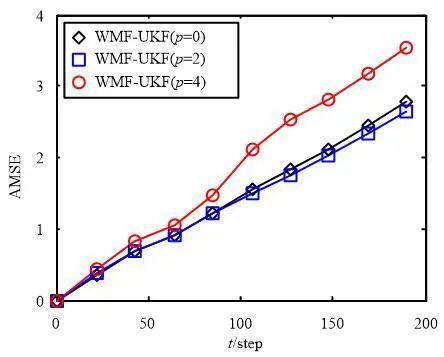
图6不同Hermite多项式下wmf-ukf位置的AMSE曲线

图6位置不同Hermite多项式的WMF-UKFs的AMSE曲线