作者:Ben Edgington;
简介
如果你想学跳曳步舞,那就错了。但相信我,ETH2的洗牌同样令人兴奋。
洗牌列表是以太坊2.0中的一个基本操作。它主要用于每12秒时隙选择验证器组成委员会,并在每个时隙选择信标链块的提议者。
混合和洗涤似乎很简单。虽然它有一些陷阱需要注意,但它们在计算机科学中是很容易理解的。金本位可能是费希尔·叶芝洗牌。那我们为什么不在ETH2中使用它呢?我将在文章的**详细解释它,但是简单地说,轻量级客户端。
我们使用的洗牌算法是swap还是not,而不是Fisher-Yates。这种选择是基于论文最初用来构建加密方案的。我最近在ETH2客户机teku中重写了我们的实现,所以我想趁热把它写出来。
交换或不洗牌算法
一轮手术
搅拌和洗涤依次进行。每一轮的过程都是一样的,所以下面我只演示一轮的过程,这比看上去简单得多。
1选择一个轴点并查找第一个镜像索引
首先,我们选择一个轴索引p,它是根据轮数和其他一些种子数据采用伪随机方法选择的。选定轴后,它将固定在圆形中。
基于这个轴心点,我们在P和0之间的中间点选择一个镜像索引M1,即M1=P/2。(为了说明,我们将忽略麻烦的一个错误舍入问题)

索引和第一个轴点
2从第一个镜像索引到轴心点,是否更换
对于镜像索引M1和轴索引p之间的每个索引,我们随机决定是否替换这些元素。
例如,对于索引I1,如果我们选择不替换它,我们将继续选择下一个索引。
如果我们决定替换,我们将把I1上的list元素替换为I1’上的list元素,也就是说,它在镜像索引上的映像。也就是说,I1被I1’=M1-(I1-M1)代替,使得I1和I1’到M1之间的距离相等。
我们对M1和P之间的每个指数做相同的交换或不交换决定。

从第一个镜像索引交换还是不交换决定
3计算第二个镜像索引
在完成从M1到P的所有索引决策之后,我们现在找到以M2为中点的第二个镜像索引,即与P和列表末尾等距的点。即M2=M1+n/2。

Nbsp;第二镜像索引
4从支点到第二个后视镜,是否更换
**,我们重复交换或不交换过程,并考虑从所有点到轴线的P替换决定,即从P到第二个镜像m2的决定。如果我们选择不替换,我们就转到下一个。如果我们选择替换,我们用镜像索引m2上J1’上的图像替换J1上的元素。
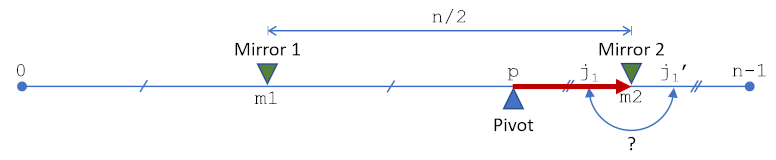
是否交换从数据透视到第二个镜像索引的决策
把它放在一起
本轮结束时,我们考虑了M1和M2之间的所有指数,也就是所有指数的一半,每一个指数在另一半都有一个具体的指数,不管是否被替代。因此,所有的指标都经过了一次是否换代的考虑。
下一轮通过增加(或减少)轮数打开,这样我们就有了一个新的轴索引,然后开始循环上述过程。
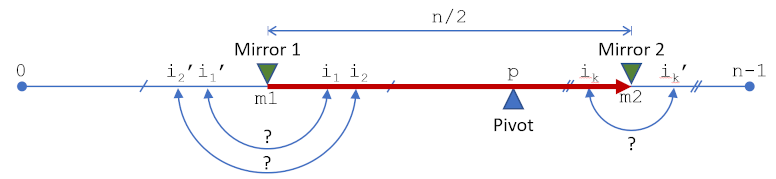
在同一轮中从一面镜子移到另一面镜子的过程
有什么有趣的
别出心裁的地方
在决定是否替换时,该算法巧妙地选择了候选索引或其图像中较高的一个。这意味着当它位于轴下方时,我被选为_1而不是I_1’;当位于轴上方时,我被选为_K’而不是I_K。这意味着我们可以灵活地遍历列表中的索引:我们可以将0到M1和P到M2分成两个独立的循环,或者将它们组合在同一个从M1到M2的循环中,正如我在上面描述(和实现的)。这两种方法的结果是一样的:不管我是考虑I_1还是mirror I_1,它是否被替换并不重要。
圆形
在ETH2中,上述过程被执行90次。原始文件中提到,需要6轮LGN回合才能“开始对选择性密码攻击有更好的安全边界”,其中n是列表的长度。在vitalik的注释规范中,他说:“密码学专家建议我们可以在4log2n轮中提供足够的安全性。”ETH2中验证器的****数量,也就是说,我们需要洗牌列表的**次数约为222(420万)。维塔利克的估计值是88轮,在论文中是92轮(假设LG是自然对数)。因此,我们现在在一个大致正确的范围内,特别是因为我们可能最终没有那么多的活动验证器。
根据列表的长度调整轮数可能会产生有趣的结果,但我们不会,这可能是一个不必要的优化。
有趣的是,当最小权威审核信标链的规范时,他们最初发现在选择块支持者的洗牌过程中存在偏差(见问题f)。但结果,他们错误地使用了只有10发子弹的混洗配置。当他们将混合配置增加到90发时(我们在主网络上使用的轮数),偏差就消失了。
(伪)随机
shuffle算法要求我们在每一轮中随机选择一个轴心点,以及是否替换每一轮中的每个元素。
在ETH2中,我们确保从种子值生成随机性,以便相同的种子总是产生相同的洗牌结果。
轴索引由种子的8字节Sha2哈希与round相串联生成,
pivot索引由8个字节的种子值Sha2散列生成,该散列与该轮相连,因此它通常在每一轮中发生变化。
用于确定是否替换元素的决定性数字是从以下元素中提取的:seed的sha256散列、round和列表中元素的索引。
效率
这种洗牌算法比Fisher-Yates算法慢得多。我们需要Fisher算法洗牌904次。我们还需要考虑伪随机性的产生,这是算法中最昂贵的部分。Fisher-Yates需要接近nlog2n位的随机性,而我们需要90位(log2n+n/2)。根据ETH2中需要的N个值的范围,多余的位相当大(当N为一百万时,ETH2大约需要N个数的两倍)。
为什么要交换呢?
如果效率不高,为什么选择这种实现方式?
单一元素混合洗涤
该算法的优点是,如果只关注几个索引,就不需要计算整个列表的洗牌。实际上,我们可以对单个索引使用此算法,以找出将要替换的索引。
因此,如果我们想知道索引217的元素在哪里被洗牌,我们可以只对该索引运行算法,而不必对整个列表进行洗牌。此外,相反,如果我们想知道哪些元素被洗牌到索引217,我们可以反向运行该算法以找到元素217(相反的意思是从高到低,而不是从低到高)。
简言之,我们可以计算元素I在哪里混合,元素I的来源在一个恒定的时间内。计算时间不取决于列表的长度。Fisher-Yates-shuffling没有这个特性,您不能对单个索引进行洗牌。他们经常需要反复地洗牌整个列表。
ETH2规范中写的是如何应用该算法来洗牌单个索引。事实上,一次洗牌整个名单只是它的一个优化!如果需要,我们可以依次洗牌列表中的一个元素:(reverse)运行shuffle以找出哪个元素在索引0中结束,然后再次运行shuffle以找出哪个元素最终位于索引1中,依此类推。我们不这样做的原因是,我们决定是否交换需要一次生成一个256位的散列,这样丢弃255位是非常浪费的。如果我们使用1位哈希或预测,洗牌一个列表元素的效率几乎和洗牌整个列表一样有效。
做一个真正的“轻”客户
这个特性之所以有意义的原因在于轻客户机。光客户端相当于ETH2信标链和碎片链的观察者。它们不存储整个状态,但希望安全地访问链上的数据。为了验证其数据的正确性,即不存在欺诈,一个必要的步骤是计算认证数据的委员会。换句话说,我们需要使用shuffle算法,我们不希望light客户端存储或洗牌整个验证器列表。有了交换或不洗牌,他们只能计算出所需的少数委员会成员,这将大大提高整体效率。
历史
如果您和我一样喜欢GitHub的考古学特性,那么您可以在这里查看关于ETH2的洗牌算法初始搜索的讨论,这里宣布了最终的赢家。
如果您想从另一个角度来看待swap或not shuffle算法,可以看看protolambda发布的更直观的解释。
**的
这张照片是在2019年,当我听Justin Drake在ETHcc上谈论交换或不洗牌时,我在teku客户端(当时也叫Artemis)中实现了第一个版本的swap or not shuffling。

文章标题:以太坊2.0的洗牌算法
文章链接:https://www.btchangqing.cn/105882.html
更新时间:2020年09月18日
本站大部分内容均收集于网络,若内容若侵犯到您的权益,请联系我们,我们将第一时间处理。

